Question

Two infinitely long parallel conducting plates having surface charge densities $+ \sigma$ and $- \sigma$ respective are separated by a small distance. The medium between the plates is vacuum. If ${\varepsilon _0}$ is the dielectric permittivity of vacuum then the electric field in the region between the plates is:

A) $0V/m$
B) $\dfrac{\sigma }{{2{\varepsilon _0}}}V/m$
C) $\dfrac{\sigma }{{{\varepsilon _0}}}V/m$
D) $\dfrac{{2\sigma }}{{{\varepsilon _0}}}V/m$

Answer 1

This problem can be solved by the applying Gauss’ theorem, “The total electric flux passing through a closed surface is equal to the $\dfrac{1}{{{\varepsilon _0}}}$ times of net charge present on the surface i.e. ${\phi _E} = \dfrac{q}{{{\varepsilon _0}}}$. It is used to determine the electric field near the infinite plane charged conducting and non-conducting parallel plates, charged conductivity and non-conductivity spherical shell etc.

Complete step by step solution:
Suppose a charge $q$ is distributed over the area $A$ uniformly then the charge per unit area is known as charge-density and it is dented by $\sigma$.
Charge density of surface $\sigma = \dfrac{q}{A}$
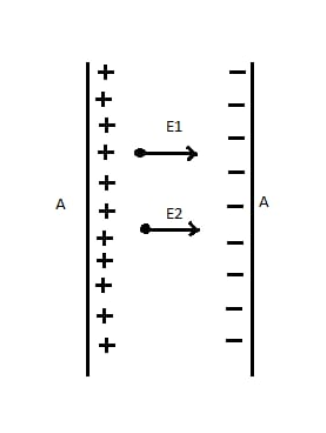
Now, suppose two infinitely long parallel conductivity plates, having surface charge density $+ \sigma$ and $- \sigma$ respectively.
We are going to find electric field intensity between both plates. Now, for this we consider only one plate. A cylindrical Gaussian surface is considered symmetrically. Both sides of plate of cross section area $d\overrightarrow A$.
So, the electric flux passes through both cross sections of the cylindrical surface.
${\phi _E} = \int_A {{E_1}.d\overrightarrow A } + \int_A {{E_1}.d\overrightarrow A } \\\ \Rightarrow {\phi _E} = {E_1}.\int_A {d\overrightarrow A } + {E_1}.\int_A {d\overrightarrow A }$
Where $\int_A {d\overrightarrow A }$ is the total area of plates.

$$\Rightarrow {\phi _E} = {E_1}.A + {E_1}A \\\ \Rightarrow {\phi _E} = 2{E_1}.A$$

So, the electric field
$\Rightarrow {E_1} = \dfrac{{{\phi _E}}}{{2A}}$.................(i)
But according to the gauss; theorem
$\Rightarrow {\phi _E} = \dfrac{q}{{{\varepsilon _0}}}$
Substituting the value of ${\phi _E}$ in equation (i)
$\Rightarrow {E_1} = \dfrac{q}{{2A{\varepsilon _0}}}$
Here, $\dfrac{q}{A}$ is called surface density. So, we can put $\sigma$for it.
Then ${E_1} = \dfrac{\sigma }{{2{\varepsilon _0}}}$.............(ii)
This is the electric field intensity due to the first plate. Similarly, electric field intensity due to second plate having surface density $- \sigma$ will be given as-
$\Rightarrow {E_2} = \dfrac{\sigma }{{2{\varepsilon _0}}}$................(iii)
The electric fields are equal because the plates have the equal surface charge density $+ \sigma$ and $- \sigma$. Now, the total electric field intensity between the plates is-
$\Rightarrow E = {E_1} + {E_2}$
${E_1}$ and ${E_2}$ are equal. So,
$\Rightarrow E = 2{E_1}$
Substituting the value of ${E_1}$, we get-
$\Rightarrow E = \dfrac{{2\sigma }}{{2{\varepsilon _0}}} \\\ \Rightarrow E = \dfrac{\sigma }{{{\varepsilon _0}}}V/m$

Hence, option C is correct.

Note: We get the maximum intensity between the plates, because electric field intensity does not depend on the sign of surface charge density that means it does not change with the positive and negative charge. It only depends on direction. Mostly, we take ${E_2}$ as negative so the resultant intensity will become zero which is incorrect. We only have to add the both intensities to get the resultant intensity.