Question
Question: Two infinitely long line charges each of linear charge density \( \lambda \) are placed at an angle ...
Two infinitely long line charges each of linear charge density λ are placed at an angle θ as shown in the figure. Find out electric field intensity at a point P , which is at a distance x from point O along the angle bisector of line charges.
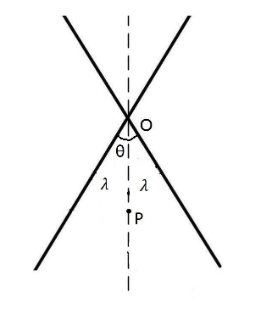
Solution
The basic physical property of matter that causes it to experience a force when kept in an electric or magnetic field is electrical charge. An electric charge is correlated with an electric field and a magnetic field is generated by the moving electric charge. The electromagnetic field is recognized as a combination of electrical and magnetic fields.
Formula Used: We will use the following formula:
E=r2kλ
Where
E is the electrical charge
λ is the linear charge density
r is perpendicular distance of the point from the line charge
k is the Coulomb’s constant.
Complete step by step solution:
Let us consider an infinitely long line charge whose linear charge density is λ
So, the magnitude of the electric field at any point at a distance of r units will be
E=r2kλ
And the direction of this electric field will be away from the wire
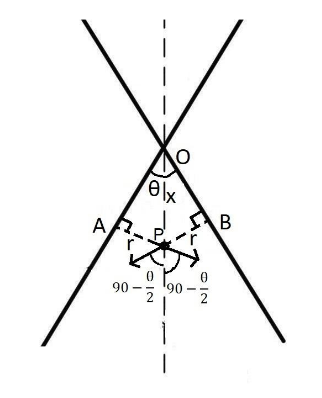
According to the question, it is given that OP=x
Let us assume that the length AP=PB=r
Now according to the figure,
xsin2θ=r
Now we know that
E=r2kλ
Now, we will replace the value of r from the above expression. So, we will get
E=xsin2θ2kλ
So, the net electrical charge will be
Enet=2Esin2θ
=2xsin2θ2kλ×sin2θ
Therefore, the magnitude of the net electrical charge will be
Enet=x4kλ
And the direction of this net charge will be along OP .
Note:
An electrical charge is a scalar quantity. In addition to having a magnitude and direction, the laws of vector addition such as triangle law of vector addition and parallelogram law of vector addition should also obey a quantity to be called a vector, only then is the quantity said to be a quantity of vector. When two currents meet at a junction, in the case of an electric current, the resulting current will be an algebraic sum and not the sum of the vector. Therefore, a scalar quantity is an electric current, although it has magnitude and direction.
