Question

Two infinitely large planes A and B intersect each other at right angles and carry uniform surface charge densities +$\sigma$ and -$\sigma$. Which of the following figures best represents electric field lines?

• A.

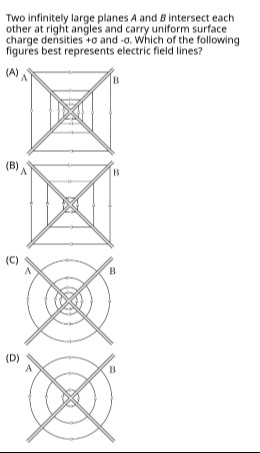
• B.

• C.

• D.

Answer 1

Answer: (B)

B

Answer 2

The problem describes two infinitely large planes, A and B, intersecting at right angles. Plane A carries a uniform surface charge density of +$\sigma$, and plane B carries a uniform surface charge density of -$\sigma$. We need to identify the figure that best represents the electric field lines.

Let's set up a coordinate system. Since the planes intersect at right angles, let's assume one plane is the y-z plane (x=0) and the other is the x-z plane (y=0).

Let Plane A be the y-z plane (x=0) with charge density +$\sigma$. Let Plane B be the x-z plane (y=0) with charge density -$\sigma$.

The electric field due to an infinite plane with uniform surface charge density $\sigma_0$ is given by $E = \frac{|\sigma_0|}{2\epsilon_0}$, and its direction is perpendicular to the plane, pointing away from a positive charge and towards a negative charge.

1. Electric Field due to Plane A (x=0, +$\sigma$):

   • For $x > 0$, the field $\vec{E}_A$ points in the $+\hat{i}$ direction: $\vec{E}_A = \frac{\sigma}{2\epsilon_0} \hat{i}$.

   • For $x < 0$, the field $\vec{E}_A$ points in the $-\hat{i}$ direction: $\vec{E}_A = -\frac{\sigma}{2\epsilon_0} \hat{i}$.

2. Electric Field due to Plane B (y=0, -$\sigma$):

   • For $y > 0$, the field $\vec{E}_B$ points in the $-\hat{j}$ direction (towards the negative plane): $\vec{E}_B = -\frac{\sigma}{2\epsilon_0} \hat{j}$.

   • For $y < 0$, the field $\vec{E}_B$ points in the $+\hat{j}$ direction (towards the negative plane): $\vec{E}_B = \frac{\sigma}{2\epsilon_0} \hat{j}$.

Now, let's find the net electric field $\vec{E} = \vec{E}_A + \vec{E}_B$ in the four quadrants of the xy-plane (assuming we are looking at a cross-section perpendicular to the intersection line, which is the z-axis). Let $E_0 = \frac{\sigma}{2\epsilon_0}$.

• Quadrant I (x > 0, y > 0):

  $\vec{E}_I = E_0 \hat{i} - E_0 \hat{j} = E_0 (\hat{i} - \hat{j})$. This vector points diagonally downwards to the right (at 45 degrees below the positive x-axis).

• Quadrant II (x < 0, y > 0):

  $\vec{E}_{II} = -E_0 \hat{i} - E_0 \hat{j} = -E_0 (\hat{i} + \hat{j})$. This vector points diagonally downwards to the left (at 45 degrees below the negative x-axis).

• Quadrant III (x < 0, y < 0):

  $\vec{E}_{III} = -E_0 \hat{i} + E_0 \hat{j} = E_0 (-\hat{i} + \hat{j})$. This vector points diagonally upwards to the left (at 45 degrees above the negative x-axis).

• Quadrant IV (x > 0, y < 0):

  $\vec{E}_{IV} = E_0 \hat{i} + E_0 \hat{j} = E_0 (\hat{i} + \hat{j})$. This vector points diagonally upwards to the right (at 45 degrees above the positive x-axis).

The electric field lines must be straight lines, parallel to the resultant field vectors in each quadrant. They originate from the positive charge (Plane A) and terminate on the negative charge (Plane B).

The electric field lines are straight and parallel in each of the four regions. The direction in each region is such that they always originate from the positive plane and terminate on the negative plane. Electric field lines from static charges cannot form closed loops.

Therefore, option (B) correctly represents the straight, parallel field lines originating from the positive plane and terminating on the negative plane in each of the four regions.