Question

Two inductors ${L_1}$ (inductance 1 mH, internal resistance $3\Omega$ ) and ${L_2}$​ (inductance 2 mH, internal resistance $4\Omega$) and a resistor R (resistance $12\Omega$) are all connected in parallel across a 5V battery. The circuit is switched on at time $t = 0$. The ratio of the maximum to the minimum current. $\dfrac{{{I_{\max }}}}{{{I_{\min }}}}$ drawn from the battery is:

Answer 1

At the time when the current starts flowing, we will have a minimum current at $t = 0$ .In this time the whole current will pass through resistance of $12\Omega$ and no current would be passing through inductors. After a long time, current will also pass through inductors, and we will have our maximum current.

Complete step by step answer:
At time $t = 0$, inductors will be acting as resistors of infinite resistance, so only current will be through the $12\Omega$ resistor. Hence it is ${I_{\min }}$.

At $t = 0$, circuit will be:

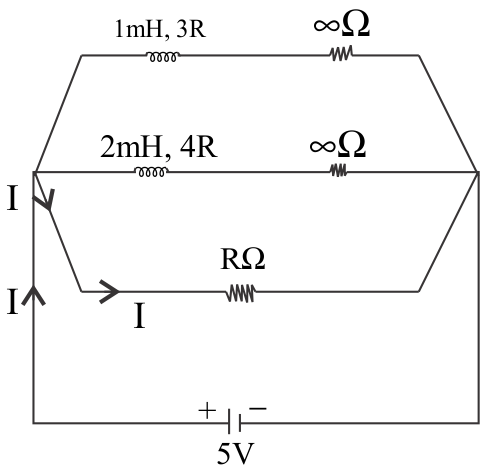
In reality, we don’t have resistances of infinite ohm with both inductors, but for visualization, both inductors will be acting as resistances of infinite ohm and there will be no current passing through them.

So using ohm’s law $V = {I_{\min }}R$, (where $V = 5$ volts and $R = 12\Omega$) we get,
${I_{\min }} = \dfrac{5}{{12}}Amp$
After a long time, inductors will not resist anymore, the only resistance will be due to their internal resistance and $12\Omega$ resistor.
After long time, equivalent circuit will be like this:

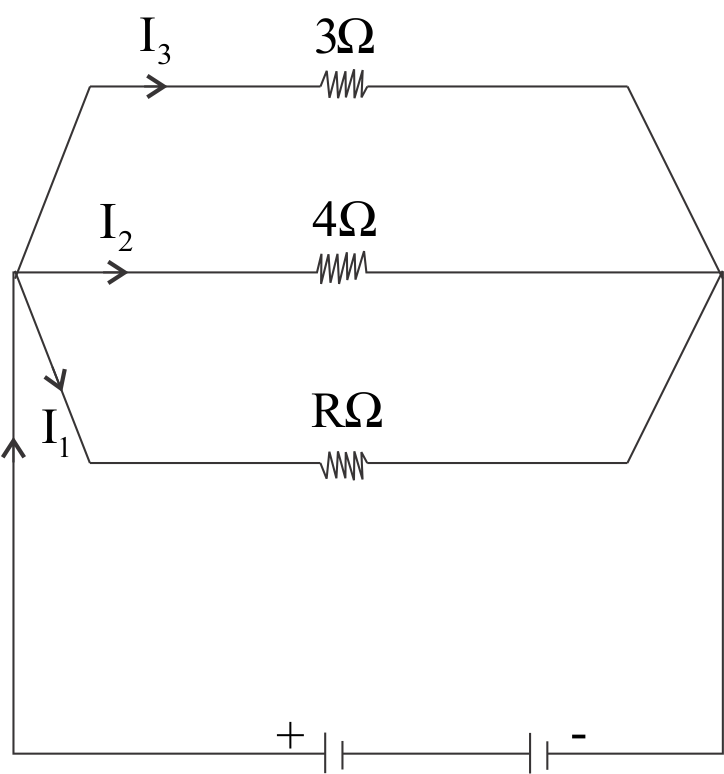
After a long time, resistance through inductors will only be due to their internal resistances and current will easily pass through them.

At that time, the equivalent resistance,
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{12}} + \dfrac{1}{3} + \dfrac{1}{4}$

On solving the above equation, we get,
$\Rightarrow$ $\dfrac{1}{{{R_{eq}}}} = \dfrac{{1 + 4 + 3}}{{12}}$
On solving this, we get equivalent resistance as,
$\Rightarrow$ $\dfrac{1}{{{R_{eq}}}} = \dfrac{8}{{12}} = \dfrac{3}{2}$

Now applying ohm’s law on $V = {I_{\max }}{R_{eq}}$, we get,
$\Rightarrow$ ${I_{\max }} = \dfrac{{5 \times 2}}{3}Amp = \dfrac{{10}}{3}Amp$
Required value $\dfrac{{{I_{\max }}}}{{{I_{\min }}}}$ will be,
$\Rightarrow\dfrac{{{I_{\max }}}}{{{I_{\min }}}} = \dfrac{{10/3}}{{5/12}} \\\ \Rightarrow\dfrac{{{I_{\max }}}}{{{I_{\min }}}} = \dfrac{{10 \times 12}}{{3 \times 5}} = 8 \\\$
So our answer is 8.

Note: At time $t = 0$, inductors will be acting as resistors of infinite resistance, so only current will be through $12\Omega$ resistor, which will give us minimum current. But after a long time, they will let the whole current pass through them and only resistance by them is due to their internal resistors and given resistance of $12\Omega$ and the current will be maximum.