Question

Two inductors each equal to $L$ are joined in parallel. The equivalent inductance is
(A) Zero
(B) $2L$
(C) $L$
(D) $\dfrac{L}{2}$

Answer 1

To solve this question, we have to use the relation between the voltage across an inductor and its inductance. Then, using the Kirchhoff’s in that formula, we can obtain the equivalent inductance for the parallel combination of the inductors.

Complete step by step answer:
Let us consider two inductors of inductances ${L_1}$ and ${L_2}$ connected to each other in a parallel combination across an alternating emf source of $V$ , as shown in the figure below.

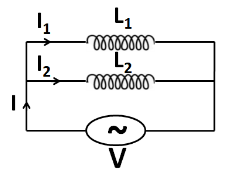
Let the current through the emf source be $I$ . Also, let us assume the currents flowing through the inductors of inductances ${L_1}$ and ${L_2}$ be ${I_1}$ and ${I_2}$ respectively. From the Kirchhoff’s voltage law, we can say that
$I = {I_1} + {I_2}$ ........................(1)
Now, we know that the voltage across an inductor is related equal to its inductance times the rate of change of the current flowing through it with time. So if the equivalent inductance is equal to ${L_{eq}}$ , then we have
$V = {L_{eq}}\dfrac{{dI}}{{dt}}$ ........................(2)
Since the inductors are connected in parallel combination across the emf source, so voltage across each inductor is equal to $V$ . So we have
$V = {L_1}\dfrac{{d{I_1}}}{{dt}}$
$\Rightarrow \dfrac{{d{I_1}}}{{dt}} = \dfrac{V}{{{L_1}}}$ ........................(3)
Similarly, we have
$\Rightarrow \dfrac{{d{I_2}}}{{dt}} = \dfrac{V}{{{L_2}}}$ ........................(4)
Substituting (1) in (2) we get
$V = {L_{eq}}\dfrac{{d\left( {{I_1} + {I_2}} \right)}}{{dt}}$
$\Rightarrow V = {L_{eq}}\left( {\dfrac{{d{I_1}}}{{dt}} + \dfrac{{d{I_2}}}{{dt}}} \right)$
Substituting (3) and (4) in the above equation, we get
$V = {L_{eq}}\left( {\dfrac{V}{{{L_1}}} + \dfrac{V}{{{L_2}}}} \right)$
$\Rightarrow \dfrac{V}{{{L_{eq}}}} = \dfrac{V}{{{L_1}}} + \dfrac{V}{{{L_2}}}$
Dividing both sides of the above equation by $V$ , we get
$\dfrac{1}{{{L_{eq}}}} = \dfrac{1}{{{L_1}}} + \dfrac{1}{{{L_2}}}$
Now, according to the question, both of the inductors have the inductance of $L$ . Therefore substituting ${L_1} = {L_2} = L$ in the above equation, we get
$\dfrac{1}{{{L_{eq}}}} = \dfrac{1}{L} + \dfrac{1}{L}$
$\dfrac{1}{{{L_{eq}}}} = \dfrac{2}{L}$
Finally taking the reciprocals of both the sides, we get
${L_{eq}} = \dfrac{L}{2}$
Thus, the equivalent inductance of the given combination is equal to $\dfrac{L}{2}$ .
Hence, the correct answer is option D.

Note:
The formulae for the equivalent inductance for the series and the parallel combination are identical to those for the resistance. In the above question, we have derived the formula for the equivalent inductance for a parallel combination. Similarly, we can also derive that in a series combination, the inductances are added.