Question

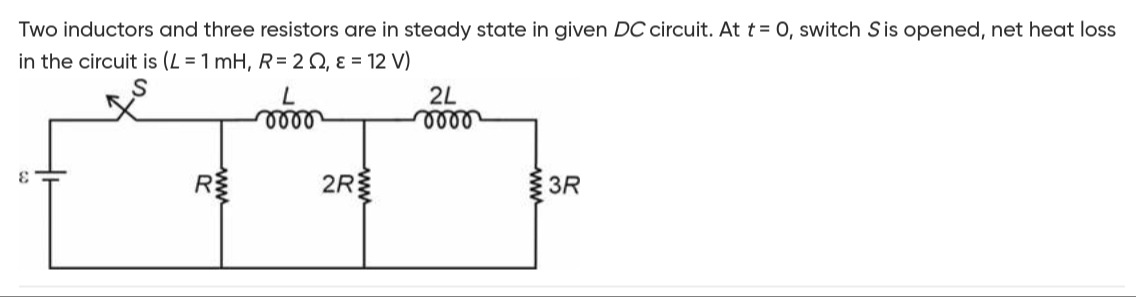
Two inductors and three resistors are in steady state in given DC circuit. At t = 0, switch S is opened, net heat loss in the circuit is (L = 1 mH, R = 2 $\Omega$, $\varepsilon$ = 12 V)

Answer 1

16.5 mJ

Answer 2

In steady state, inductors act as short circuits. When the switch S is closed, the potential at nodes A, B, and C is $\varepsilon$. Currents through resistors: $I_R = \frac{\varepsilon}{R}$, $I_{2R} = \frac{\varepsilon}{2R}$, $I_{3R} = \frac{\varepsilon}{3R}$. Current through L: $I_L = \frac{5\varepsilon}{6R}$. Current through 2L: $I_{2L} = \frac{\varepsilon}{3R}$.

Initial energy stored in inductors: $U_{initial} = \frac{1}{2}LI_L^2 + \frac{1}{2}(2L)I_{2L}^2$ $U_{initial} = \frac{1}{2}L \left(\frac{5\varepsilon}{6R}\right)^2 + L \left(\frac{\varepsilon}{3R}\right)^2$ $U_{initial} = \frac{11}{24} L \frac{\varepsilon^2}{R^2}$

Substitute values: $L = 1 \times 10^{-3} \text{ H}$, $R = 2 \Omega$, $\varepsilon = 12 \text{ V}$. $U_{initial} = \frac{11}{24} \times (1 \times 10^{-3}) \times \frac{(12)^2}{(2)^2} = \frac{11}{24} \times 10^{-3} \times \frac{144}{4} = \frac{11}{24} \times 10^{-3} \times 36 = 16.5 \times 10^{-3} \text{ J} = 16.5 \text{ mJ}$.

The net heat loss is equal to the initial energy stored.