Question
Question: Two independent harmonic oscillators of equal mass are oscillating about the origin with angular fre...
Two independent harmonic oscillators of equal mass are oscillating about the origin with angular frequencies ω1 and ω2 and have total energies E1 and E2, respectively. The variations of their momenta p with positions x are shown in figures. If ba=n2 and Ra=n, then the correct equation(s) is (are)
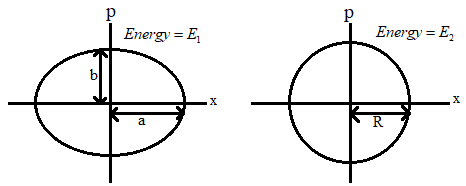
A. E1ω1=E2ω2B. ω1ω2=n2C. ω1ω2=n2D. ω1E1=ω2E2
Solution
We have two different particles undergoing independent harmonic oscillations and the mass of them are the same. We are given the angular frequencies and energies of the two systems. From the given figure we can identify their path and find the maximum momenta and their energies, then by using the given relations we will get the correct expressions.
Formula used:
p=mv
E=21mω2a2
Complete step-by-step answer:
In the question we are given two independent harmonic oscillations with equal mass.
The angular frequencies of the two oscillations are ω1 and ω2 and their energies are E1 and E2 respectively.
Let us consider the first case.
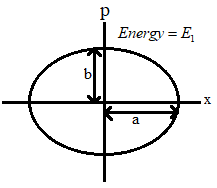
From the figure we can see that the particle in this oscillation has an elliptical path.
We know that the momentum is given by the equation,
p=mv, were ‘m’ is the mass and ‘v’ is the velocity.
Therefore the maximum momentum will be,
pmax=mvmax
Since the maximum velocity, vmax=rω, were ‘r’ is the radius and ‘ω’ is the angular frequency, we get the maximum momentum as,
pmax=mrω
Therefore in the first case, since it is an elliptical path the radius is taken as ‘a’ and from the figure we can see that ‘b’ is the maximum momentum.
Therefore we get,
⇒pmax=b=maω1
Now let us consider case 2.
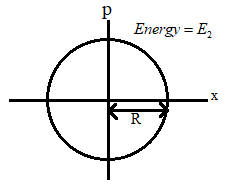
From the figure we can see that the particle in this oscillation has a circular path.
We know that the maximum momentum is,
pmax=mrω
In this case, from the figure we can see that the radius and the maximum momentum is ‘R’. therefore we get,
⇒pmax=R=mRω2
⇒mω2=1
Thus we have the maximum momentum in case 1 and 2 as b=maω1 and mω2=1 respectively.
By dividing these two equations we get,
⇒1b=mω2maω1
Since the mass is equal in both the cases. We can eliminate the mass.
⇒ab=ω2ω1
In the question it is given that ba=n2
Therefore we know that, ab=n21
By substituting this we will get,
⇒ω2ω1=ab=n21
⇒ω2ω1=n21
Therefore we get,
⇒ω1ω2=n2
Hence option B is correct.
Now let us consider the energy in both the cases.
In the first case, we will get the energy as,
E1=mω12a2
E2=mω22R2
By dividing these two equations, we will get
⇒E2E1=mω22R2mω12a2
⇒E2E1=ω22R2ω12a2
From the question we know that, Ra=n
Therefore we know that ⇒R2a2=n2
Thus the ratio of the energies will become,
⇒E2E1=ω22ω12×n2
From previous calculation we know that,
n2=ω1ω2
By substituting this in the ratio equation, we will get
⇒E2E1=ω22ω12×ω1ω2
⇒E2E1=ω2ω1
⇒ω1E1=ω2E2
Therefore option D is also correct.
So, the correct answer is “Option B and D”.
Note: A periodic oscillation is an oscillation when the periodic motion repeats at fixed intervals. Simple harmonic motion or SHM is a special type of periodic oscillation. In simple harmonic motion the restoring force of the moving object will be always directly proportional to the magnitude of displacement of the object and its direction will be toward the mean position.
