Question
Question: Two identified parallel plate capacitors A and B are connected to a battery of V volts with the swit...
Two identified parallel plate capacitors A and B are connected to a battery of V volts with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant K. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.
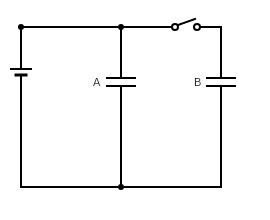
Solution
It is given that when the switch is closed, there is a current V flowing through the capacitors. Find the total energy by adding up the energy contributed by each capacitor. When the switch is opened and the di-electric is filled in between, calculate the total energy in this case and find the ratio of the same.
Complete step by step answer
When switch S is closed, there is a current I flowing through the circuit which has a potential difference of V volts from the source. Energy emitted by a capacitor in this case is expressed as the product of its capacitance and the square of the voltage flowing through the capacitor. This is mathematically represented as ,
⇒Q=21CV2 (where C is the capacitance of the capacitor and V is the voltage flowing across)
Now when switch S is closed, the total energy given out by the system is given as,
⇒E=QA+QB
Where QA is energy given out by capacitor A and QB is energy given out by capacitor B.
⇒QA=QB=21CV2
The overall energy can be written as ,
⇒E=CV2
Now, when the switch is open and the di-electric of di-electric constant K is inserted between the parallel plate capacitors, there will be a flow of voltage V across the capacitor A. Whereas in capacitor B the stored voltage will be flowing across the plates, which is denoted by V′ . Now , total energy of the system is again the sum of the individual energy possessed by the capacitors
⇒E′=QA+QB
Now, energy across the capacitor A is given as,
⇒QA=21(KC)V2 , Where K is the di-electric constant.
In case of capacitor B, the voltage flowing across the plates will be the stored voltage V′ . This can be represented as V′=KV . Using this, the energy across capacitor B is,
⇒QB=21(KC)V′2
On substituting and cancelling the common term, we get,
⇒QB=21KCV2
Now total energy E′ is given as,
⇒E′=QA+QB
On substituting ,
⇒E′=21KCV2+21KCV2
Taking the common term, we get,
⇒E′=21CV2(K+K1)
On simplifying, we get,
⇒E′=21CV2(KK2+1)
Now, the ratio between the first and second case is given as ,
⇒E′E=21CV2(KK2+1)CV2
On removing the common term and taking the denominator term to numerator , we get,
⇒E′E=K2+12K
Hence, the ratio of the total electrostatic energy stored in both capacitors before and after introduction of di-electric is found out.
Note
In a parallel plate capacitor setup, the capacitance depends upon the charge flowing between the plate and the Voltage applied through the circuit, the area between the plate and the permissibility factor.
