Question

Two identical wires A and B, each of length L, carry the same current I. Wire A is bent into a circle of radius R and wire B is bent to form a square of side ‘a’. If ${{B}_{A}}$ and ${{B}_{B}}$ are the values of magnetic field at the centre of the circle and square respectively, then what is the value of the ratio $\dfrac{{{B}_{A}}}{{{B}_{B}}}$?
A. $\dfrac{{{\pi }^{2}}}{8\sqrt{2}}$
B. $\dfrac{{{\pi }^{2}}}{8}$
C. $\dfrac{{{\pi }^{2}}}{16\sqrt{2}}$
D. $\dfrac{{{\pi }^{2}}}{16}$

Answer 1

Use expressions of magnetic field at the centre of the circular loop and magnetic field at the centre of the square to obtain ${{B}_{A}}$ and ${{B}_{B}}$. Then take their ratio to obtain the result. Alternatively, We can also use Biot-Savart Law to find magnetic fields at centres of the circle and square. Biot-Savart law describes the magnetic field at a point due to a small current carrying segment. This segment is considered as vector quantity and its direction is along the direction of current.
Formula used:
Magnetic field in case of circle of radius R, $B=\dfrac{{{\mu }_{0}}I}{2R}$; Magnetic field in case of square of side a, $B=\dfrac{4{{\mu }_{0}}I}{\pi a\sqrt{2}}$

Complete answer:
Both wires carry current I and are of length L.
Magnetic field for a circle of radius R is given by
$B=\dfrac{{{\mu }_{0}}I}{2R}$
Length of wire A is L and when the wire is bent into a circular loop its perimeter is equal to length of wire.
$2\pi R=L\Rightarrow R=\dfrac{L}{2\pi }$

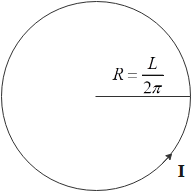
Therefore, magnetic field due to a circle formed by wire A
${{B}_{A}}=\dfrac{{{\mu }_{0}}I}{2R}=\dfrac{{{\mu }_{0}}I}{2\dfrac{L}{2\pi }}=\dfrac{\pi {{\mu }_{0}}I}{L}$
Length of wire B is L and when the wire is bent into a square loop its perimeter is equal to length of wire.
$4a=L\Rightarrow a=\dfrac{L}{4}$

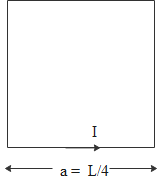
Therefore, magnetic field due to a square formed by wire B
${{B}_{B}}=\dfrac{4{{\mu }_{0}}I}{\pi a\sqrt{2}}=\dfrac{4{{\mu }_{0}}I}{\pi \dfrac{L}{4}\sqrt{2}}=\dfrac{16{{\mu }_{0}}I}{\pi L\sqrt{2}}$
Taking ratios of ${{B}_{A}}$ and ${{B}_{B}}$, we get
$\dfrac{{{B}_{A}}}{{{B}_{B}}}=\dfrac{\dfrac{\pi {{\mu }_{0}}I}{L}}{\dfrac{16{{\mu }_{0}}I}{\pi L\sqrt{2}}}=\dfrac{\pi {{\mu }_{0}}I}{L}\times \dfrac{\pi L\sqrt{2}}{16{{\mu }_{0}}I}$
On simplifying
$\dfrac{{{B}_{A}}}{{{B}_{B}}}=\dfrac{{{\pi }^{2}}}{8\sqrt{2}}$

So, the correct answer is “Option A”.

Note:
When two identical wires with same current flowing through them are bent to form square loop and circular loop respectively. The magnetic field due to the circular loop is approximately 0.87 times the magnitude of the magnetic field at the centre of the square.