Question
Question: Two identical uniform solid spherical balls A and B of mass m each are placed on a fixed wedge as sh...
Two identical uniform solid spherical balls A and B of mass m each are placed on a fixed wedge as shown in figure. Ball B is kept at rest and it is released just before two balls collide. Ball A rolls down without slipping on an inclined plane and collides elastically with ball B. The kinetic energy of ball A just after the collision with ball B is:
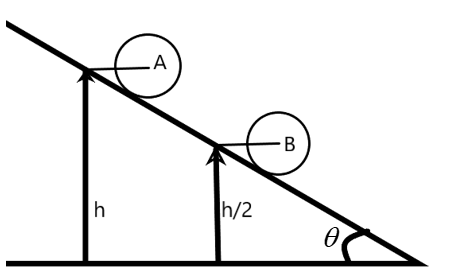
Solution
We are to use the conservation laws of linear momentum and kinetic energy to find the solution to the problem. We can equate the kinetic energies of the two balls before and after collision to find the velocity of each ball, and thereby find the kinetic energy of ball A.
Complete answer:
In the situation given here, the ball is undergoing a rotational motion along with the translation motion, so we have to consider the moment of inertia element of the ball A before the collision to get the correct answer. We know that the moment of inertia of a sphere rotating along the axis that passes through the center of the sphere is given by –
I=52mr2
The kinetic energy of the ball related to the rotational energy is given by –
KErot=21I(rvcm)2=5mvcm2
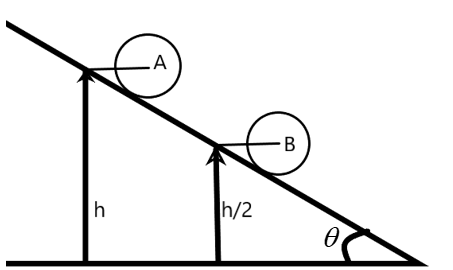
The ball loses its potential as it moves down the height, which is converted to the kinetic energy. So the kinetic energy possessed by the ball A while it collides the ball B at the height 2h is given by –
Potential energy lost by the ball A is equal to the kinetic energy gained buy the ball A.
i.e.,
