Question

Two identical trains P and Q move with equal speeds on parallel tracks along the equator. P moves from east to west and Q moves from west to east. Which of the following conclusions can be drawn from this data?
A) Data is insufficient to arrive at a conclusion.
B) Both exert equal force on the track.
C) Train Q exerts a greater force on the track.
D) Train P exerts a greater force on the track.

Answer 1

Earth rotates from west to east. So the effective velocity of the two trains moving from east to west and from west to east will change according to the velocity of the earth. The weight of the train will be balanced by the normal force and the centripetal force acting on the train.

Formula used:
-The centripetal force acting on a body is given by, ${F_c} = \dfrac{{m{v^2}}}{r}$ where $m$ is the mass of the body, $v$ is the velocity of the body and $r$ is the distance from the centre of rotation of the body.

Complete step by step answer.
Step 1: Sketch a figure describing the motion of the two trains along the equator.

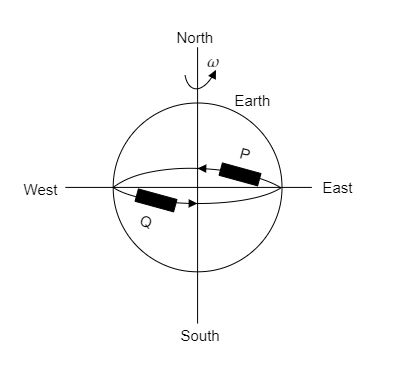
In the above figure, $\omega$ is the angular velocity of the earth. Then the linear velocity of the earth will be $v = \omega r$ where $r$ is the radius of the earth.
Here train P moves from east to west while train Q moves from west to east.
It is mentioned that the two trains are identical and are moving with the same speeds.
If ${M_P}$ and ${M_Q}$ are the masses of the trains P and Q then we have ${M_P} = {M_Q} = M$.
Also if ${v_P}$ and ${v_Q}$ are the velocities of the trains P and Q then we have ${v_P} = {v_Q} = {v_{train}}$ .
As the earth rotates from west to east, the effective velocity of train P which moves from east to west will be ${v_{P.eff}} = {v_{train}} - v$ .
Since the train Q moves from west to east, its effective velocity will be ${v_{Q.eff}} = {v_{train}} + v$ .
So the effective velocity of train Q will be greater than that of train P i.e., ${v_{Q.eff}} > {v_{P.eff}}$ .
Step 2: List the forces acting on the two trains and obtain the force balance equation.
The forces acting on each train are its weight, a normal force exerted on the train by the track and centripetal force.
Now the weight of the two trains will be the same and given by $W = Mg$ .
Let ${N_P}$ and ${N_Q}$ be the normal force acting on trains P and Q respectively.
The centripetal forces of the two trains P and Q can be expressed as ${F_P} = \dfrac{{M{{\left( {{v_{P.eff}}} \right)}^2}}}{r}$ and ${F_Q} = \dfrac{{M{{\left( {{v_{Q.eff}}} \right)}^2}}}{r}$ respectively.
The force balance equation of train P is given by, $Mg = {N_P} + {F_P} = {N_P} + \dfrac{{M{{\left( {{v_{P.eff}}} \right)}^2}}}{r}$
$\Rightarrow {N_P} = Mg - \dfrac{{M{{\left( {{v_{P.eff}}} \right)}^2}}}{r}$ -------- (1)
The force balance equation of train Q is given by, $Mg = {N_Q} + {F_Q} = {N_Q} + \dfrac{{M{{\left( {{v_{Q.eff}}} \right)}^2}}}{r}$
$\Rightarrow {N_Q} = Mg - \dfrac{{M{{\left( {{v_{Q.eff}}} \right)}^2}}}{r}$ --------- (2)
Now since ${v_{Q.eff}} > {v_{P.eff}}$ , the normal force on train P will be more than that on train Q.

So the correct option is D

Note: Since ${v_{Q.eff}} > {v_{P.eff}}$ , the centripetal force of train Q will be more than that of train P i.e., ${F_Q} = \dfrac{{M{{\left( {{v_{Q.eff}}} \right)}^2}}}{r} > {F_P} = \dfrac{{M{{\left( {{v_{P.eff}}} \right)}^2}}}{r}$ . So the force balance equation of train Q given by equation (2) suggests that a greater number has to be subtracted from the weight of the train to obtain the normal force acting on Q. So we conclude that the normal force on train P is greater than that on Q.