Question
Question: Two identical thin uniform rods of length L each are joined to form T shape as shown in the figure. ...
Two identical thin uniform rods of length L each are joined to form T shape as shown in the figure. The distance of the centre of mass from D is
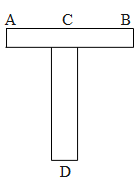
(1)0(2)4L(3)43L(4)L
Solution
Hint : We know that the centre of mass of a body is the point where the whole mass of the body is concentrated. Thus for a system of particles this point is called the point of centre of mass. Thus in order to find the centre of mass of a T shaped rod, then first we have to find the centre of mass of the individual rod. Then find the centre of mass along the vertical rod, we will get the solution.
Complete step-by-step solution:
Given that the length of the rod is L. Hence its centre of mass lies at the half length 2L.
The centre of mass along the vertical line is,
yCM=m1+m2m1y1+m2y2
yCM=2m0+2mL
yCM=4L
Hence here the centre of mass of the system lies at the lower end of the rod. Thus The distance of the centre of mass from D is 4L.
Therefore option (2) is correct.
Note: So we calculate the centre of mass of every object by simply knowing their masses and multiplying them by their positions. Besides the pure geometric method we can also find the centre of gravity of any object by the plum line method. For a sphere of uniform density the centre of mass lies at the geometric centre of the sphere.
