Question

Two identical thin rings each of radius ‘R’ are coaxially placed at a distance R apart. If $Q_1\ and\ Q_2$are respectively the charges uniformly spread on the two rings, the work done in moving a charge ‘q’ from the centre of one ring to the other is:
$\text{A.}\quad \dfrac{q(Q_1/Q_2)(\sqrt2+1)}{4\pi\epsilon_{\circ}\sqrt2 R}$
$\text{B.}\quad \dfrac{q(Q_1-Q_2)(\sqrt2-1)}{4\pi\epsilon_{\circ}\sqrt2 R}$
$\text{C.}\quad \dfrac{q(Q_1+Q_2)\sqrt2}{4\pi\epsilon_{\circ} R}$
$\text{D.}\quad zero$

Answer 1

Potential energy is a quantity which defines the stability of the system. If it is less, the system is stable and if it is more, the system is unstable. P.E. can be positive, negative or zero. A positive potential energy is when two charges/bodies repel each other due to their nature whereas negative potential energy signifies that there is attraction between two bodies.
Formula used:
$Work\ done = q\Delta V$, potential at a co-axial distance of a uniformly charged ring = $\dfrac{Kq}{d}$

Complete answer:
This question could be easily solved by finding the potential at the centre of any ring.

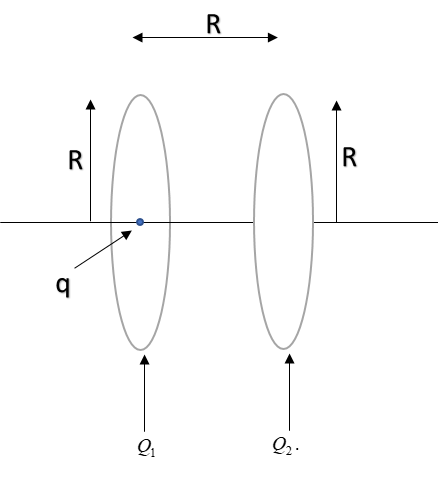
Potential at the centre of a ring will be the sum of potential of the individual ring at that point.
$V_{Total} (at\ the\ centre\ of\ Q_1) = \dfrac{KQ_1}{R} + \dfrac{KQ_2}{d}$

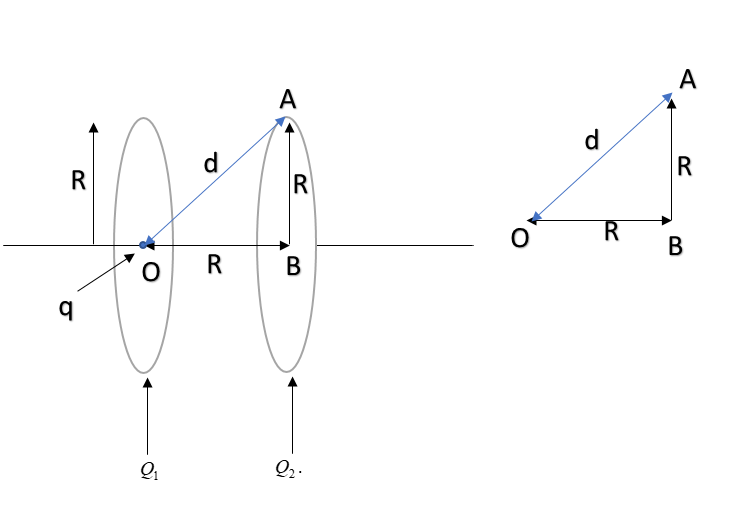
Now, from geometry we can see that in right angled $\Delta ABO$, $d = \sqrt{R^2+R^2} = \sqrt2 R$
Thus, $V_{total\ Q_1} = \dfrac{KQ_1}{R} + \dfrac{kQ_2}{\sqrt2 R} = \dfrac{K}{R}\left[ Q_1 + \dfrac{Q_2}{\sqrt2}\right]$
By, symmetry, we can write $V_{Total\ Q_2} = \dfrac{K}{R}\left( Q_2 + \dfrac{Q_2}{\sqrt2} \right)$
Now, using $Work\ done = q\Delta V$, where ‘q’ is the charge to be moved and $\Delta V$being the change in the potential, we get;
$W = q\times \left[\dfrac{K}R \left( Q_1 + \dfrac{Q_2}{\sqrt2} \right) - \dfrac{K}{R}\left(Q_2 + \dfrac{Q_1}{\sqrt2} \right)\right]$
$W = \dfrac{Kq(Q_1-Q_2)}{R} \times (1-\dfrac{1}{\sqrt2})$
As $K = \dfrac{1}{4\pi\epsilon_{\circ}}$
Hence $W = \quad \dfrac{q(Q_1-Q_2)(\sqrt2-1)}{4\pi\epsilon_{\circ}\sqrt2 R}$.

So, the correct answer is “Option B”.

Note:
These types of questions are very easy. No need for integration and we can get the answers. Students should realize that work done on any charge is given by $Work\ done = q\Delta V$. We just have to take the difference in potential of two points. This is the advantage of a state function or path function, we just have to take the difference between two points and we are done. Hence electrostatic work is a state function. Students just need to remember the potential due to different bodies at a particular point.