Question
Question: Two identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by t...
Two identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation of the either ball from vertical when each thread makes a small angle 'θ' with the vertical?
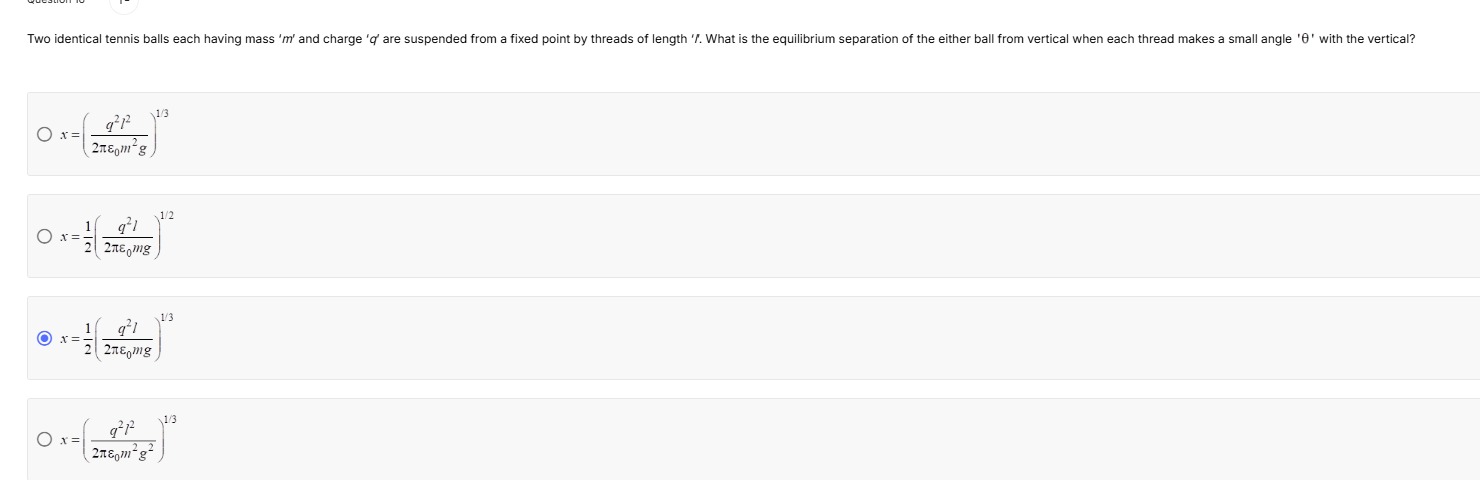
x = (2πϵ0m2gq2l2)1/3
x = 21(2πϵ0mgq2l)1/2
x = 21(2πϵ0mgq2l)1/3
x = (2πϵ0m2g2q2l2)1/3
x = $\frac{1}{2}\left(\frac{q^2l}{2\pi\epsilon_0mg}\right)^{1/3}
Solution
Let the mass of each ball be m and the charge be q. The length of the thread is l. Let the equilibrium separation between the two balls be x. When the thread makes a small angle θ with the vertical, the horizontal distance of each ball from the vertical line passing through the suspension point is lsinθ. Thus, the separation between the two balls is x=2lsinθ.
Each ball is in equilibrium under the action of three forces:
- Tension T in the thread.
- Gravitational force mg acting vertically downwards.
- Electrostatic force Fe due to the other ball, acting horizontally away from the other ball.
Resolving the tension into vertical and horizontal components, we have:
Vertical equilibrium: Tcosθ=mg
Horizontal equilibrium: Tsinθ=Fe
Dividing the second equation by the first, we get:
tanθ=mgFe
The electrostatic force between the two charges is given by Coulomb's law:
Fe=4πϵ01x2q⋅q=4πϵ0x2q2
Substituting this into the equilibrium equation:
tanθ=4πϵ0x2mgq2
We are given that the angle θ is small. For small angles, tanθ≈sinθ.
Also, from the geometry, the horizontal distance of each ball from the vertical is x/2. So, sinθ=lx/2=2lx.
Using the small angle approximation tanθ≈sinθ:
2lx≈4πϵ0x2mgq2
Now, we solve for x:
x⋅x2=4πϵ0mgq2⋅2l
x3=4πϵ0mg2q2l
x3=2πϵ0mgq2l
Taking the cube root of both sides:
x=(2πϵ0mgq2l)1/3
The question asks for the equilibrium separation of either ball from vertical, which is x/2.
Therefore, x/2=21(2πϵ0mgq2l)1/3
