Question

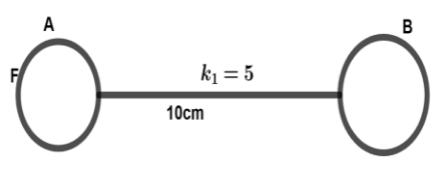
Two identical spheres $A$ and $B$ having an equal charge repel with each other with force $100\,N$. When they are placed $10\,cm$ apart in a medium of dielectric constant 5. Now, determine charge on each sphere:

Answer 1

Coulomb's law states, the magnitude electrostatic force of attraction or repulsion. Two electrical charged bodies is directly proportional to product of the charged bodies and inversely proportional to the square of the distance between the Centre charged bodies.

Complete step by step answer:
Given that two spheres $A$ and $B$ having equal charges,
Here $F$ is force with $100\,N$
Medium dielectric constant is ${k_1} = 5$
Distance between these two spheres is $10\,cm$.

From coulomb's law, we know that
$F = \dfrac{{k{q^2}}}{{{k_1}{r^2}}}$
Here $q$ represents quantity of charges,
Where as, we known from coulomb’s law constant,
$k = \dfrac{1}{{4\pi {e_o}}}$
Now substitute all the values in $F$, then we get
$100 = \dfrac{1}{{4\pi {e_o}}} \times \dfrac{{{q^2}}}{{5{{(10 \times {{10}^{ - 2}})}^2}}}$
From coulombs theorem we know,
$k = \dfrac{1}{{4\pi eo}} = 9 \times {10^9}$
Now we get,
100 = \dfrac{{9 \times {{10}^9} \times {q^2}}}{{5 \times {{\left( {10 \times {{10}^{ - 2}}} \right)}^2}}} \\\ \Rightarrow {q^2} = \dfrac{{100 \times 5 \times {{10}^{ - 2}}}}{{9 \times {{10}^9}}} \\\ \Rightarrow {q^2} = \dfrac{{100 \times 5}}{9} \times {10^{ - 11}} \\\ \Rightarrow {q^2} = \dfrac{{500}}{9} \times {10^{ - 11}} \\\
$\therefore q = 23.9 \sim 10\,C$

Additional information: Coulombs discovered by the 1785 by French physicist Charles Augustin de Coulomb. This law is essential for the theory of electromagnetism. Coulombs value is approximately $k = 9 \times {10^9}$. Coulomb's law is stated as the simple mathematical expression. From Coulomb's law we can define the Scalar form of the law and Vector form of the law. Coulomb's law holds even with the atoms. Gauss’s law can be derived from Coulomb's law and Coulombs can be derived from Gauss’s law .

Note: Gauss’s law can be derived from Coulomb's law and Coulombs can be derived from Gauss’s law. If any two spheres repel each other with the same force and apart some distance in medium of dielectric constant then we can calculate and solve it by using Coulomb's law. In order to find out the extent of repulsion or attraction.