Question

Two identical resistors each of resistance $10\,\,ohm$ are connected 1) in series 2) in parallel, in line to a battery of $6\,v$ . Calculate the ratio of power consumed in the series and parallel combination:

Answer 1

Hint
In order to find the ratio of power that is consumed by the series combination and the parallel combination, we have to divide the power in the series combination to the power in the parallel combination. The current passing through the circuits of series and parallel are different from each other. The power consumed in the circuit can be found by,
$P = V \times I$
Where, $P$ denotes the power consumed by the circuit,, $V$ denotes the voltage of the battery,, $I$ denotes the current across the circuit.

Complete step by step solution
Given that,
Resistor of resistance ${R_1} = 10\,\,ohm$,
Resistor of resistance ${R_2} = 10\,\,ohm$,
Battery of voltage $V = 6\,v$.
(1) Series circuit:
__
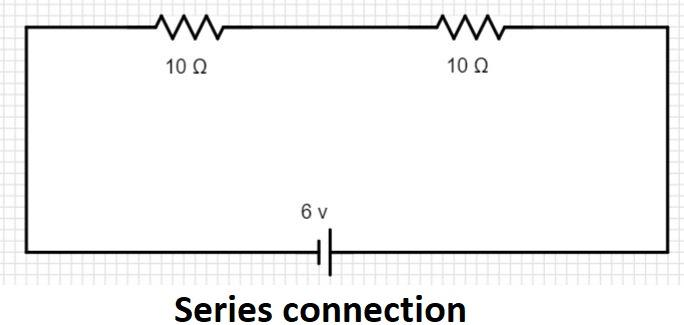
To find the total resistance of a circuit in series connection;
${R_s} = {R_1} + {R_2}$
Where, ${R_s}$ denotes the resistance of the resistor in a series circuit,
${R_1}$ denotes the first resistor,
${R_2}$ denotes the second resistor.
Substitute the values for ${R_1}$ and ${R_2}$ ;
${R_s} = 10\,\,ohm + 10\,\,ohm$
${R_s} = 20\,\,ohm$
The resistance of a resistor connected in a series circuit is ${R_s} = 20\,\,ohm$ .
The current across the series circuit is;
$I = \dfrac{V}{{{R_s}}}$
Substitute the values of battery voltage and resistance of a resistor in series;
$I = \dfrac{{6\,\,v}}{{20\,\,ohm}}$
By dividing we get;
$I = 0.3\,\,A$
The current across the series circuit is $I = 0.3\,\,A$ .
To find the power consumption in series circuit;
${P_1} = V \times I$
Where,
${P_1}$ is the power in series connection.
${P_1} = 6\,\,v \times 0.3\,\,A$
${P_1} = 1.8\,\,W$
(2) Parallel circuit:
__
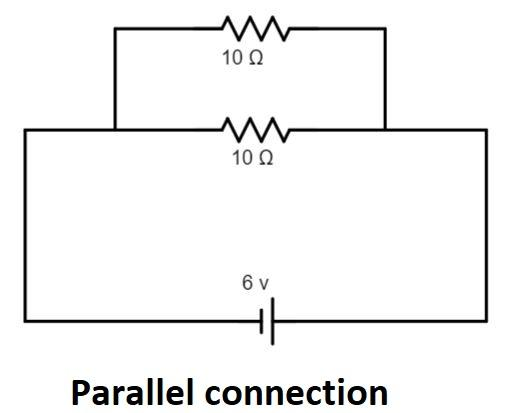
To find the total resistance of a circuit in parallel connection;
$\dfrac{1}{{{R_p}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
Where, ${R_p}$ denotes the resistance of the resistor in a parallel circuit,
${R_1}$ denotes the first resistor,
${R_2}$ denotes the second resistor.
Substitute the values for ${R_1}$ and ${R_2}$;
$\dfrac{1}{{{R_p}}} = \dfrac{1}{{10\,\,ohm}} + \dfrac{1}{{10\,\,ohm}}$
Simplifying the equation;
$\dfrac{1}{{{R_p}}} = \dfrac{2}{{10}}$
Since we only need ${R_p}$ ,
Reciprocate the terms on both sides;
${R_p} = \dfrac{{10}}{2}$
${R_p} = 5\,\,ohm$
The resistance of a resistor connected in a parallel circuit is ${R_p} = 5\,\,ohm$ .
The current across the parallel circuit is;
$I = \dfrac{V}{{{R_p}}}$
Substitute the values of battery voltage and resistance of a resistor in parallel;
$I = \dfrac{{6\,\,v}}{{5\,\,ohm}}$
By dividing we get;
$I = 1.2\,\,A$
The current across the parallel circuit is $I = 0.3\,\,A$ .
To find the power consumption in parallel circuit;
${P_2} = V \times I$
Where,
${P_2}$ is the power in series connection.
${P_2} = 6\,\,v \times 1.2\,\,A$
${P_2} = 7.2\,\,W$
To find the ratio between the power consumption in series circuit and power consumption in parallel circuit is;
$\dfrac{{{P_1}}}{{{P_2}}} = \dfrac{{1.8\,\,W}}{{7.2\,\,W}}$
That is the ratio between the power consumption in series circuit and power consumption in parallel circuit is $0.25\,\,W$ .

Note
The equation $I = \dfrac{V}{R}$which denotes the current is derived from the Ohm’s law formula that is $V = I \times R$ and it has a relation with the power $P$ . This is because the power is directly in proportion to the voltage $V$ of the current $I$ flowing across it.