Question

Two identical positive charges are placed on the $y$ axis at $y=-a$ and $y=+a$. The variation of $V$ (electric potential) along $x$ axis is shown by graph:
A.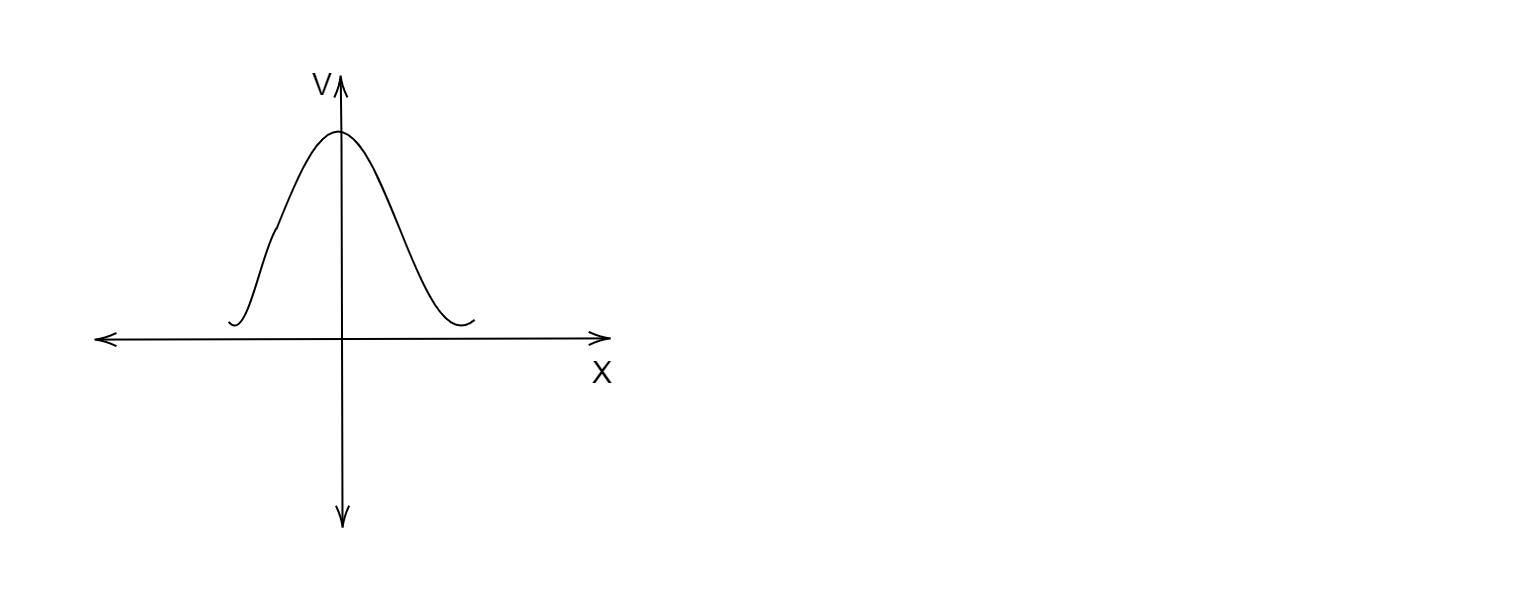
B.
C.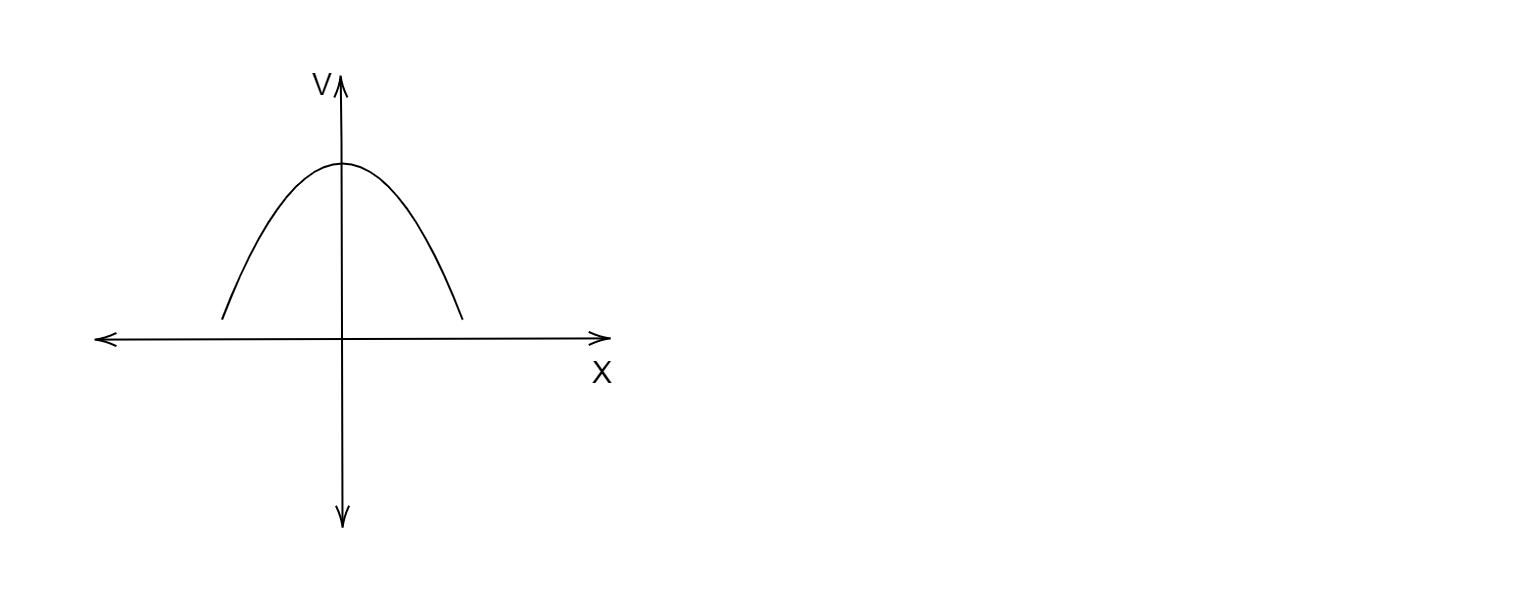
D.

Answer 1

To know about the variation of electric potential along the $x$ axis can be found out by calculating electric potential at different points on the $x$ axis. We can calculate the electric potential at a random point on the $x$ axis first and then use it to find the variation of electric potential.

Complete answer:
Let us first consider a random point on the $x$ axis. Let the random point at which we will find the electric potential be at the point $(x,0)$ and let us call it $P$.

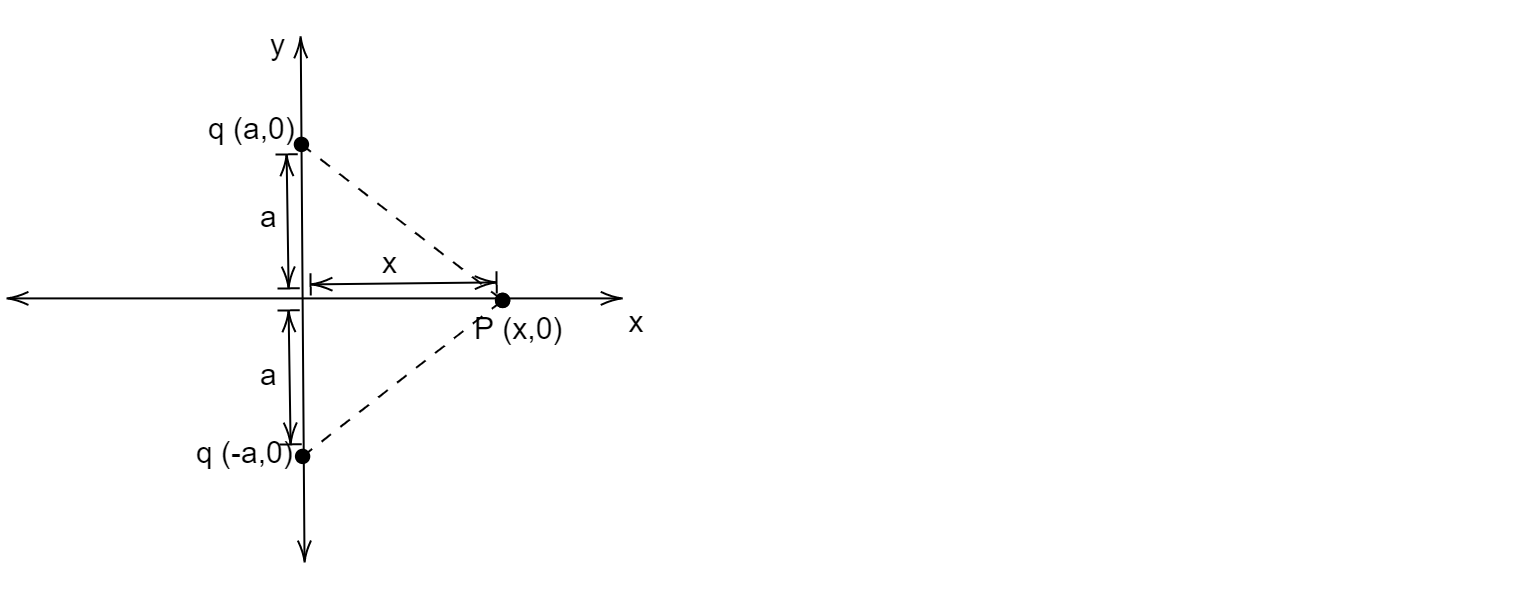
The distance $d$ of the point $P$ from the two identical positive charges can be found out by Pythagorean theorem:
$d=\sqrt{{{a}^{2}}+{{x}^{2}}}$
The electric potential at point $P$ due to the positive charge placed at $y=-a$ will be:
${{V}_{1}}=\dfrac{kq}{\sqrt{{{a}^{2}}+{{x}^{2}}}}$
The electric potential at point $P$ due to the positive charge placed at $y=+a$ will be:
${{V}_{2}}=\dfrac{kq}{\sqrt{{{a}^{2}}+{{x}^{2}}}}$
The total electric potential at point $P$ due to both the positive charges will be:
$\begin{aligned} & {{V}_{total}}={{V}_{1}}+{{V}_{2}} \\\ & {{V}_{total}}=\dfrac{kq}{\sqrt{{{a}^{2}}+{{x}^{2}}}}+\dfrac{kq}{\sqrt{{{a}^{2}}+{{x}^{2}}}} \\\ & {{V}_{total}}=\dfrac{2kq}{\sqrt{{{a}^{2}}+{{x}^{2}}}} \\\ \end{aligned}$
At origin, when $x=0$, the total electric potential will be:
$\begin{aligned} & {{V}_{total}}=\dfrac{2kq}{\sqrt{{{a}^{2}}+{{0}^{2}}}} \\\ & {{V}_{total}}=\dfrac{2kq}{\sqrt{{{a}^{2}}}} \\\ & {{V}_{total}}=\dfrac{2kq}{a} \\\ \end{aligned}$
When $x\to \infty$, the total electric potential will be:
$\begin{aligned} & {{V}_{total}}=\dfrac{2kq}{\sqrt{{{a}^{2}}+{{x}^{2}}}} \\\ & {{V}_{total}}=\dfrac{2kq}{x\sqrt{\dfrac{{{a}^{2}}}{{{x}^{2}}}+\dfrac{{{x}^{2}}}{{{x}^{2}}}}} \\\ & {{V}_{total}}=\dfrac{2kq}{x\sqrt{0+1}} \\\ & {{V}_{total}}=\dfrac{2kq}{x} \\\ & {{V}_{total}}\to 0 \\\ \end{aligned}$
Now we need to find the graph that matches the value of the electric potential that we found out for electric potential at $x=0$ and $x\to \infty$. If we observe carefully, then graph $A$ acquires a maximum value at $x=0$ and a minimum value at $x\to \infty$.

Therefore, the correct option is $A$.

Note:
Students might get confused between option $A$ and option $C$ but we must also see that the electric potential is inversely proportional to the distance on $x$ axis, therefore the graph must be a rectangular hyperbola, thus option $A$ must be correct.