Question

Two identical particles move towards each other with velocity $2v$ and $v$ respectively. The velocity of centre of mass is-
A. $V$
B. $\dfrac{V}{3}$
C. $\dfrac{V}{2}$
D. Zero

Answer 1

When working with a system of particles, the centre of mass notion is quite beneficial. In this lesson, we'll look at the centre of mass's velocity when two identical particles move toward each other with respective velocity.

Complete step by step answer:
The rate at which an object's position varies over time is called velocity. A system's centre of mass is the point of particles within it where all of the system's mass is concentrated. When the system of particles moves, the centre of mass moves with it. The centre of mass velocity equation is the sum of each particle's momentum (mass times velocity) divided by the total mass of the system.

Now, let us solve the given question; let's say each body has a mass of $m$ . The diagram depicts their movements.

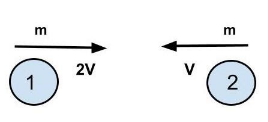
The velocity of the centre of mass of three particles is shown in this equation:
${V_{CM}} = \dfrac{{{m_1}{v_1} + {m_2}{v_2}}}{{{m_1} + {m_2}}}$
Where:
$m$ stands for mass in kilogrammes $\left( {kg} \right)$
$v$ denotes the speed in metres per second $\left( {m{s^{ - 1}}} \right).$
So, putting the value in the equation;
${V_{CM}} = \dfrac{{{m_1}{v_1} + {m_2}{v_2}}}{{{m_1} + {m_2}}}$
$\Rightarrow {V_{CM}} = \dfrac{{m \times 2V - mV}}{{m + m}} \\\ \therefore {V_{CM}}= \dfrac{V}{2}$
As a result, the centre of mass's velocity is $\dfrac{V}{2}$.

So, the correct option is C.

Note: One thing should be noted that the first particle's motion is assumed to be positive. As a result, the system's centre of mass has a velocity of $\dfrac{V}{2}$ in the direction of motion of the particle with the higher speed.