Question

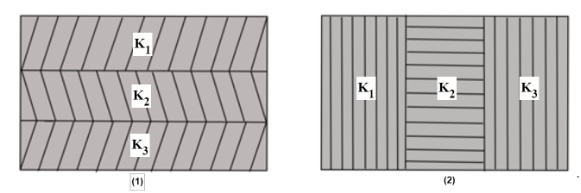
Two identical parallel plate capacitors, of capacitance $C$ each, have plates of area $A$ , separated by a distance $d$ . the space between the plates of two capacitors is filled with three dielectrics of equal thickness and dielectric constants ${K_1},{K_2}\& {K_3}$. The first capacitor is filled as shown in fig(1) and the second one is filled as shown in fig(2).

If these two modified capacitors are charged by the same potential $V$ , the ratio of the energy stored in the two would be :
A. $\dfrac{{{E_1}}}{{{E_2}}} = \dfrac{{{K_1}{K_2}{K_3}}}{{\left( {{K_1} + {K_2} + {K_3}} \right)\left( {{K_1}{K_2} + {K_2}{K_3} + {K_1}{K_3}} \right)}} \\\$
B. $\dfrac{{{E_1}}}{{{E_2}}} = \dfrac{{\left( {{K_1} + {K_2} + {K_3}} \right)\left( {{K_1}{K_2} + {K_2}{K_3} + {K_1}{K_3}} \right)}}{{{K_1}{K_2}{K_3}}} \\\$
C. $\dfrac{{{E_1}}}{{{E_2}}} = \dfrac{{9{K_1}{K_2}{K_3}}}{{\left( {{K_1} + {K_2} + {K_3}} \right)\left( {{K_1}{K_2} + {K_2}{K_3} + {K_1}{K_3}} \right)}} \\\$
D. $\dfrac{{{E_1}}}{{{E_2}}} = \dfrac{{\left( {{K_1} + {K_2} + {K_3}} \right)\left( {{K_1}{K_2} + {K_2}{K_3} + {K_1}{K_3}} \right)}}{{9{K_1}{K_2}{K_3}}}$

Answer 1

To find the ratio of energy stored in the capacitors, we have to use the concept of energy stored in capacitor, capacitance of capacitor filled with dielectrics and the series and parallel combinations of the capacitors. The capacitance of the capacitor is directly proportional to the area of the plates and inversely proportional to the separation between the plates of the capacitor.

Formulae used:
Energy stored in a capacitor is given by
$E = \dfrac{1}{2}C{V^2}$
Where, $C$ - capacitance of the capacitor charged by the potential $V$.
Series combination of capacitors,
$\dfrac{1}{{{C_{equ}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}}$
Parallel combination of capacitors,
${C_{equ}} = {C_1} + {C_2} + {C_3}$
The capacitance of the capacitor is given by
$C = \dfrac{{A{\varepsilon _0}K}}{d}$
Where, $A$ - area of the plates, $d$ - separation between plates and $K$ - dielectric constant.

Complete step by step answer:

Let us consider the first diagram in which dielectrics are connected in series.
So, the capacitance of each capacitor having dielectric is
${C_1} = \dfrac{{3A{\varepsilon _0}{K_1}}}{d}$ , ${C_2} = \dfrac{{3A{\varepsilon _0}{K_2}}}{d}$ and ${C_3} = \dfrac{{3A{\varepsilon _0}{K_3}}}{d}$
The equivalent capacitance of these capacitors is
$\dfrac{1}{{{C_{equ}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}}$
Substituting the values, we get
${C_{equ}} = \dfrac{{3{\varepsilon _0}A{K_1}{K_2}{K_3}}}{{d({K_1}{K_2} + {K_2}{K_3} + {K_1}{K_3})}} - - - - - - - - (1)$
Now, consider the second figure in which dielectrics are connected in parallel.So, capacitance of each capacitor having dielectric is

\Rightarrow {C_1} = \dfrac{{A{\varepsilon _0}{K_2}}}{{3d}},{C_3} \\\ \Rightarrow {C_1} = \dfrac{{A{\varepsilon _0}{K_3}}}{{3d}}$$ The equivalent capacitance of these capacitors will be ${C_{equ}} = {C_1} + {C_2} + {C_3}$ Substituting the values, we get $C_{equ}^{''} = \dfrac{{{\varepsilon _0}A}}{{3d}}({K_1} + {K_2} + {K_3}) - - - - - - - - (2)$ Now, The ratio of energy stored in each case is given by $\dfrac{{{E_1}}}{{{E_2}}} = \dfrac{{\dfrac{1}{2}{C_{equ}}{V^2}}}{{\dfrac{1}{2}C_{equ}^{''}{V^2}}} \\\ \Rightarrow \dfrac{{{E_1}}}{{{E_2}}}= \dfrac{{{C_{equ}}}}{{C_{equ}^{''}}}$ Using equation $(1)\& (2)$ , we get $\therefore \dfrac{{{E_1}}}{{{E_2}}} = \dfrac{{9{K_1}{K_2}{K_3}}}{{\left( {{K_1} + {K_2} + {K_3}} \right)\left( {{K_1}{K_2} + {K_2}{K_3} + {K_1}{K_3}} \right)}}$ **Hence, option C is correct.** **Note:** The area of the dielectric is not same for both cases also, the thickness of the dielectric changes in both cases. As capacitance of the capacitor is directly proportional to the area of the plates and inversely proportional to the separation between the plates of capacitor, the capacitance changes for both cases. The potential applied to both the capacitors is the same and hence it is constant for both cases.