Question

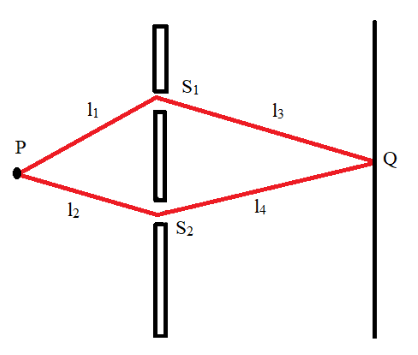
Two identical narrow slits ${S_1}$ and ${S_2}$ are illuminated by light of wavelength $\lambda$ from a point source $P$. If, as shown in the diagram above the light is then allowed to fall on a screen, and if $n$ is a positive integer, the condition for destructive interference at $Q$ is
A. $({l_1} + {l_2}) - ({l_3} + {l_4}) = \left( {2n + 1} \right)\dfrac{\lambda }{2}$
B. $({l_1} - {l_2}) = \left( {2n + 1} \right)\dfrac{\lambda }{2}$
C. $({l_3} - {l_4}) = \left( {2n + 1} \right)\dfrac{\lambda }{2}$
D. $({l_1} + {l_3}) - ({l_2} + {l_4}) = \left( {2n + 1} \right)\dfrac{\lambda }{2}$

Answer 1

There will exist a path difference between the two paths of light since both are coming from different locations. This path difference is responsible for the superposition of two waves of light to produce either constructive or destructive interference. The equation for the path difference which is obtained from its definition is equated to the formula of path difference for destructive interference to obtain the answer.

Formula used:
This equation for path difference is given by:
$p = \left( {2n - 1} \right)\dfrac{\lambda }{2}$
Where, $p$ is the path difference, $\lambda$ is the wavelength and $n$ is a positive integer.

Complete step by step answer:
When two monochromatic light sources emerging from two narrow slits placed symmetrically above one another, is said to superimpose one another to produce an interference pattern wherein the type of interference is either constructive or destructive in nature. The above problem revolves around the concept behind this principle which was used in the Young’s Double Slit experiment. The given is also an example of the same experiment.

First, let us look into the concept of interference of light. The phenomenon of interference occurs when two light waves of identical frequency with no phase difference or some value of phase difference, traversing in the same direction superimpose each other which is what occurs here. This superimposition results in a set of alternating bright and dark fringes to be formed on the screen which is known as the interference pattern.

The waves of the light from the two slits are said to interact with each other in accordance with the superposition principle. This superimposition results in the intensity of light in that region to become maximum or minimum at certain points in the pattern.

As per the law of superposition principle when two waves meet in the same phase, that is, when the crest of one wave falls over the crest of another wave or when trough of one wave falls over the trough of another wave their displacements are added up hence the phenomenon of constructive interference takes place making the fringe in that region to be dark.

As per the law of superposition principle when two waves meet in opposite phases that is a phase of ${180^ \circ }$ that is when the crest of one wave falls over the trough of another their displacements are deducted hence the phenomenon of destructive interference takes place making the fringe in that region to be dark. This is what we are required to produce as per the question. We are asked to take only the destructive interference resulting in production of dark fringes into consideration.

Since the light is emerging from two different points there will be a difference in their path which means there will be a path difference between the two light sources. There will be a certain amount of difference in wavelengths of the two lights which is given by its path difference. Hence, we can say that:
$p = P{S_1}Q - P{S_2}Q$------($1$)
It is hence given by the difference in their total lengths which is given to us.
The total path length of the first light wave will be given by:
$P{S_1}Q = {l_1} + {l_3}$------($2$)
The total path length of the second light wave will be given by:
$P{S_2}Q = {l_2} + {l_4}$------($3$)
By substituting the equations ($2$) and ($3$) in equation ($1$) we can say that by definition of path difference which is given by the difference in its lengths we can say that the total path difference of these two light sources will become:
$p = ({l_1} + {l_3}) - ({l_2} + {l_4})$-------($4$)

Since the nature of interference is directly dependent on the path difference, there is a formula for the path difference for destructive interference to occur. This equation for path difference is given by:
$p = \left( {2n - 1} \right)\dfrac{\lambda }{2}$
Since this is just the odd multiple of the wavelength we can write:
$p = \left( {2n + 1} \right)\dfrac{\lambda }{2}$ -------($5$)
This is also used to represent odd numbers.
Since equations ($4$) and ($5$) are identical we equate them to get:
$({l_1} + {l_3}) - ({l_2} + {l_4}) = \left( {2n + 1} \right)\dfrac{\lambda }{2}$
This is our final equation that will be obtained.

Therefore, the correct option is option D.

Note: There are only certain conditions under which the interference phenomenon takes place. The light used to produce the interference pattern on the screen is said to be monochromatic in nature which means that the light should be of one color with a single frequency. To produce sustained interference or in other words permanent interference is produced only when the two sources of light used must be coherent in nature, that is, they must have constant phase difference between them.