Question

Two identical metal beads each of mass $190g$ of small diameter can move along a smooth, thin uniform glass rod kept horizontal. The mass of the thin rod is $60g$ and the length is $L$. The rod is capable of rotating about the vertical axis which is passing through its centre. Initially the beads are very close to the axis of rotation and the rod is rotated at a speed of $40rad{{s}^{-1}}$. Find the variation in the angular speed of the system, if the beads have moved up to the ends of the rod because of the centrifugal force. Whether rotational kinetic energy is conserved or not? Justify your answer. Suppose that no external torque acts on the system.

Answer 1

In this case angular momentum will be conserved since there is no torque applied on the system. Initially the beads are at the axis of rotation so the moment of inertia of beads will be zero. Hope these may help you to solve this question.

Complete step by step answer:

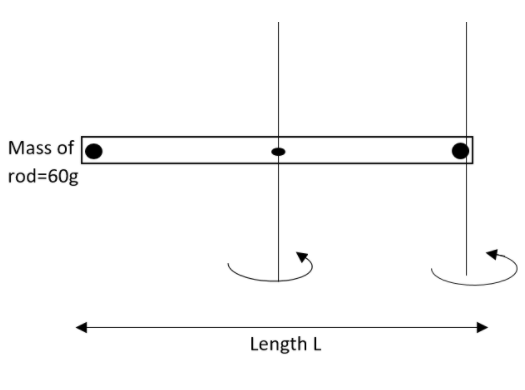
Here angular momentum is conserved due the zero torque applied on the system. As the beads are at the axis of rotation, their moment of inertia will be zero. Therefore the moment of inertia at this situation will be the moment of inertia due to the rod about axis passing through centre which is given as,
$I=\dfrac{1}{12}m{{L}^{2}}$
When the beads are at the end, the moment of inertia will be,
$\begin{aligned} & {{I}_{f}}=\dfrac{1}{12}m{{L}^{2}}+2{{m}_{b}}{{\left( \dfrac{L}{2} \right)}^{2}} \\\ & {{I}_{f}}=\dfrac{1}{12}m{{L}^{2}}+\dfrac{1}{2}{{m}_{b}}{{L}^{2}} \\\ \end{aligned}$
Here the mass of the rod is,
$m=60g$
And the mass of the bead is
${{m}_{b}}=190g$
Initial angular velocity of the rod is,
${{\omega }_{i}}=40rad{{s}^{-1}}$
Therefore, we can write that,
${{I}_{i}}{{\omega }_{i}}={{I}_{f}}{{\omega }_{f}}$
Substituting the values in it,
$\dfrac{1}{12}m{{L}^{2}}\times 40=\left( \dfrac{1}{12}m{{L}^{2}}+\dfrac{1}{2}{{m}_{0}}{{L}^{2}} \right){{\omega }_{f}}$
Simplifying the equation will give,
$200{{L}^{2}}=100{{L}^{2}}\times {{\omega }_{f}}$
Therefore the final angular velocity is,
${{\omega }_{f}}=2rad{{s}^{-1}}$
The initial kinetic energy of the system can be written as,
${{K}_{1}}=\dfrac{1}{2}{{I}_{i}}{{\omega }_{i}}^{2}$
Substituting the values in it,
${{K}_{1}}=\dfrac{1}{2}\times 60\times {{L}^{2}}\times 1600=48000{{L}^{2}}$
The final kinetic energy will be,
${{K}_{2}}=\dfrac{1}{2}\times {{I}_{f}}\times {{\omega }_{f}}^{2}$
Substituting the values in it,
$\begin{aligned} & {{K}_{2}}=\left[ \dfrac{1}{2}\times 60\times {{L}^{2}}+\dfrac{1}{2}\times 190\times {{L}^{2}} \right]\times {{2}^{2}} \\\ & {{K}_{2}}=500{{L}^{2}} \\\ \end{aligned}$
That means the kinetic energy of the system will not be conserved.

Note: Angular momentum is also known as rotational momentum. It is analogous to linear momentum in classical physics. Angular momentum is a conserved quantity as long as any external torque acts on the system.