Question

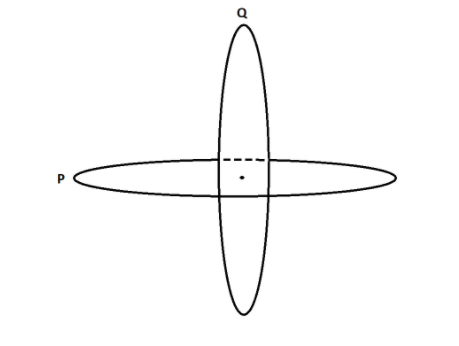
Two identical loops $P$ and $Q$ each of radius $5cm$ are lying in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common center of the two coils, if they carry currents equal to $3A$ and $4A$ respectively.

Answer 1

Hint We are given here with two similar loops with some amount of current flowing through it. We are asked to calculate the magnitude and direction of the net magnetic field on their common centre. Thus, we will use the formula for magnetic field due to a current carrying loop.
Formulae Used
$B = \dfrac{{{\mu _o}I}}{{2R}}$
Where, $B$ is the magnetic field on the point, $I$ is the current flowing through the loop and $R$ is the radius of the loop.

Complete Step By Step Solution
Here,
We redraw the diagram taking into account the flow of the current in the two.

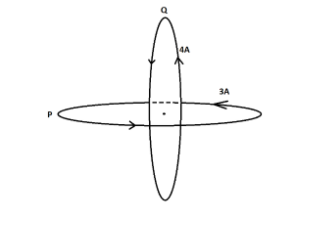
Now,
We use the right hand thumb rule and then find the magnetic field on the centre due to the individual loops.
Thus,
The diagram turns out to be

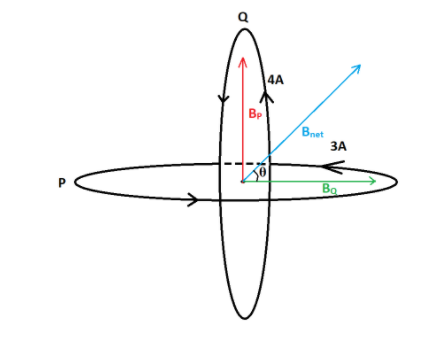
${B_P}$ is the magnetic field on the centre due to loop$P$.
${B_Q}$ is the magnetic field due to loop$Q$.
And, ${B_{net}}$ is the net magnetic field on the common centre.
$\theta$ is the direction of the net magnetic field. Basically, the angle of the net magnetic field with the horizontal.
Now,
As per the formula,
${B_p} = \dfrac{{{\mu _o}(3)}}{{2(5 \times {{10}^{ - 2}})}}$
${B_Q} = \dfrac{{{\mu _o}(4)}}{{2\left( {5 \times {{10}^{ - 2}}} \right)}}$
Thus,
${B_{net}} = \sqrt {{B_P}^2 + {B_Q}^2}$
Thus, substituting the values in the formula, we get
${B_{net}} = \dfrac{{{\mu _o}}}{{2\left( {5 \times {{10}^{ - 2}}} \right)}}\sqrt {{3^2} + {4^2}}$
Thus, we get
${B_{net}} = \dfrac{{{\mu _o}}}{{2 \times {{10}^{ - 2}}}}$
We know,
${\mu _o} = 4\pi \times {10^{ - 7}}$
Thus, we get
${B_{net}} = 2\pi \times {10^{ - 7}} \times {10^2}$
Thus, we get the magnitude as
${B_{net}} = 2\pi \times {10^{ - 5}}T$
Now,
For finding the direction, we proceed with
$\tan \theta = \dfrac{{{B_P}}}{{{B_Q}}}$
Substituting the values of ${B_P}$ and${B_Q}$, we get
$\tan \theta = \dfrac{3}{4}$
Thus, we get
$\theta = {\tan ^{ - 1}}\left( {\dfrac{3}{4}} \right)$

Note Here we have considered the direction of the flow of current as per the diagram above. But if the directions were something different from our direction, though the methodology remained the same. The magnitude would be calculated to be the same but the direction will differ by a general branch value of ${\tan ^{ - 1}}\left( 0 \right)$.