Question

Two identical light waves having phase difference $\phi$ propagate in same direction. When they superpose, the intensity of resultant wave is proportional to

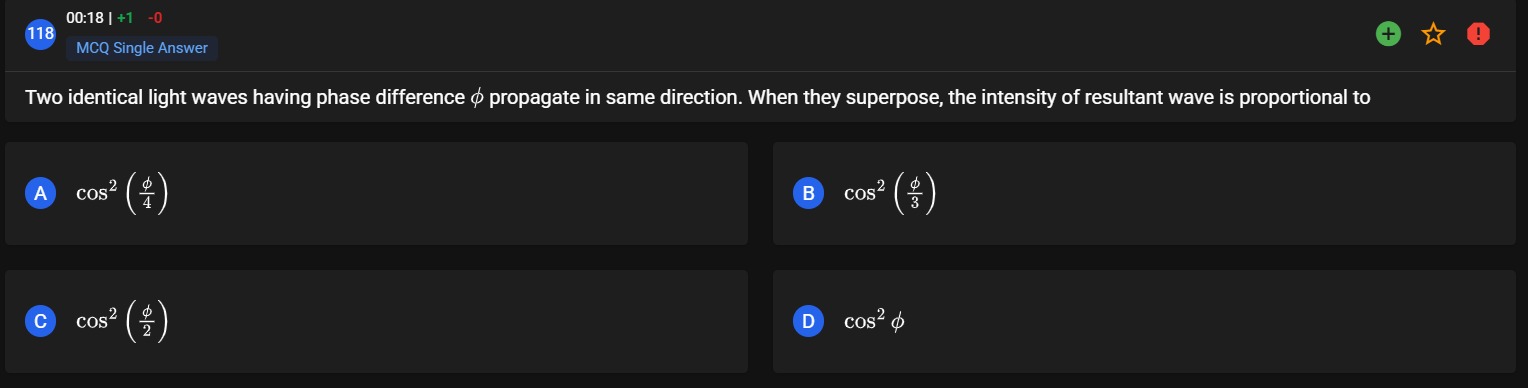
• A. $\qquad cos^2(\frac{\phi}{4})$
• B. $\qquad cos^2(\frac{\phi}{3})$
• C. $\qquad cos^2(\frac{\phi}{2})$
• D. $\qquad cos^2\phi$

Answer 1

Answer: (C)

Option C

Answer 2

When two identical light waves of amplitude $A$ have a phase difference $\phi$, the net amplitude $R$ is given by:

$$R = 2A \cos\left(\frac{\phi}{2}\right)$$

Thus, the intensity (which is proportional to $R^2$) becomes:

$$I \propto R^2 = 4A^2 \cos^2\left(\frac{\phi}{2}\right)$$

Since $4A^2$ is a constant factor, the intensity is proportional to:

$$\cos^2\left(\frac{\phi}{2}\right)$$