Question

Two identical glass rods ${S_1}$and ${S_2}$(refractive index=1.5) have one convex end of radius of curvature 10 cm. They are placed with curved surfaces at a distance d as show in the figure, with their axes aligned. When a point source of light P is placed inside rod ${S_1}$on its axis at a distance of 50 cm from the curved face, the light rays emanating from it are found to be parallel to the axis inside ${S_2}$. The distance d is

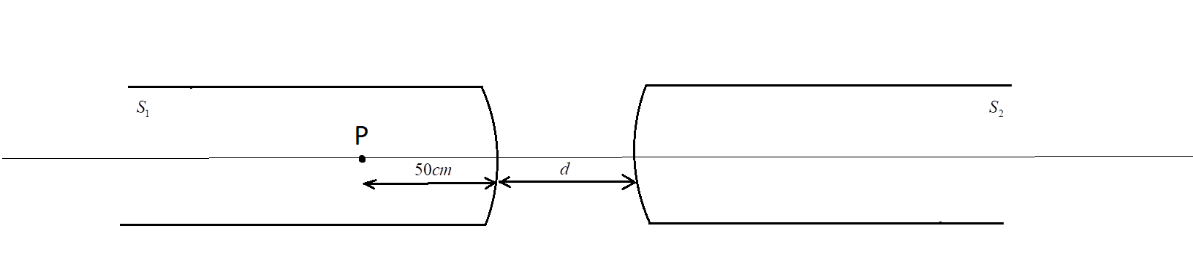
A. 60 cm B. 70 cm C. 80 cm D. 90 cm

Answer 1

For this problem, the formula for refraction at spherical surfaces should be used.
$\dfrac{{{n_2}}}{v} - \dfrac{{{n_1}}}{u} = \dfrac{{{n_2} - {n_1}}}{R}$
where ${n_1}$= refractive index of the first medium where object is present ${n_2}$= refractive index of the second medium where image is present $u$= distance of object from pole $v$= distance of image from pole $R$= radius of curvature of the spherical surface

Complete step by step answer:
Step 1: Consider the refraction at ${S_1}$
At the spherical surface ${S_1}$,
Object is at the distance, $u = - 50cm$
Refractive index of first medium, ${n_1} = 1.5 \to (glass)$
Refractive index of second medium, ${n_2} = 1 \to (air)$
Radius of curvature, $R = 10cm$

Let us apply the formula for refraction at a spherical surface to find the distance of the image formed.
$\dfrac{{{n_2}}}{v} - \dfrac{{{n_1}}}{u} = \dfrac{{{n_2} - {n_1}}}{R} \\\ \dfrac{1}{v} - \dfrac{{1.5}}{{\left( { - 50} \right)}} = \dfrac{{1 - 1.5}}{{\left( { - 10} \right)}} \\\ Solving, \\\ \dfrac{1}{v} = - \dfrac{{0.5}}{{ - 10}} + \left( {\dfrac{{1.5}}{{ - 50}}} \right) \\\ \dfrac{1}{v} = \dfrac{{0.5}}{{10}} - \dfrac{{1.5}}{{50}} \\\ \dfrac{1}{v} = \dfrac{{2.5 - 1.5}}{{50}} \\\ v = \dfrac{{50}}{1} = 50cm \\\$
Thus, the image at ${S_1}$ is formed at a distance of 50cm from the ${S_1}$.

Step 2: Consider the refraction at ${S_2}$
The image formed at ${S_1}$acts as the object for the surface ${S_2}$
At the spherical surface ${S_2}$,
Object is at $u = - (d - 50)$
Image is formed at $v = \infty$
Refractive index of first medium, ${n_1} = 1 \to (air)$
Refractive index of second medium, ${n_2} = 1.5 \to (glass)$
Radius of curvature, $R = 10cm$
Let us apply the formula for refraction at a spherical surface to find the distance of the image formed.
$\dfrac{{{n_2}}}{v} - \dfrac{{{n_1}}}{u} = \dfrac{{{n_2} - {n_1}}}{R} \\\ \Rightarrow \dfrac{{1.5}}{\infty } - \dfrac{1}{{\left( { - (d - 50)} \right)}} = \dfrac{{1.5 - 1}}{{10}} \\\$
Solving,
$\dfrac{1}{{d - 50}} = \dfrac{{0.5}}{{10}} - {{\dfrac{{1.5}}{\infty }}}0 \\\ \Rightarrow \dfrac{1}{{d - 50}} = \dfrac{{0.5}}{{10}} \\\$
Cross - multiplying,
$\left( {d - 50} \right)0.5 = 10 \\\ \Rightarrow \left( {d - 50} \right) = \dfrac{{10}}{{0.5}} \\\ \Rightarrow \left( {d - 50} \right) = 20 \\\ \Rightarrow d = 50 + 20 = 70cm \\\$
Hence, the correct option is Option B.

Note: In this problem, the first surface ${S_1}$ is a concave surface and ${S_2}$ is a convex surface. Therefore, the radius of curvature for the concave surface is negative (-) and the radius of curvature for the convex surface is (+). The students should be very careful in substituting the values because of the sign convention involved.
The best practice to follow is to first substitute the entire value with a sign inside the brackets.
For example, if $u = - 10cm$, it is better to substitute it as $\left( { - 10} \right)$ in the first step instead of taking the minus sign out in the first step itself, like $- \left( {10} \right)$. This will ensure that you don’t make any calculation errors.