Question
Question: Two identical discs of the same radius \( R \) are rotating about their axes in opposite directions ...
Two identical discs of the same radius R are rotating about their axes in opposite directions with the same constant angular speed ω . The discs are in the same horizontal plane. At the time t=0 , the points P and Q are facing each other as shown in the figure. The relative speed between the two points P and Q is vr . In one time period (T) of rotation of the discs, vr as a function of time is best represented by
(A) 
(B) 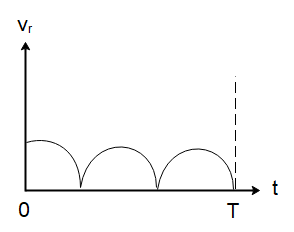
(C) 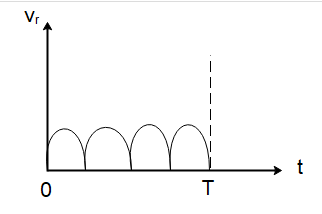
(D)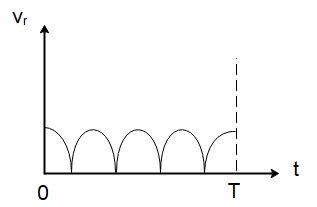
Solution
Hint : In this solution, we will determine the relative positions of points P and Q and write the relative velocity in terms of a periodic function. We will then determine the relative time period of the relative velocity.
Complete step by step answer
In a point on a circle, its velocity will always be tangential to the circle in the direction in which it is rotating. In the scenario given to us, the two circles are rotating in opposite directions.
Since both the circles have opposite circular velocity, the relative velocity of points P and Q will be
ωr=2ωr
Then the relative angle between the velocity vector of the two points will
θ=ωrt
Hence the relative velocity will be the resultant velocity vector as
∣vr∣=v2+v2−2vvcos(2ωrt)
⇒∣vr∣=2v2×(1−2cos(2ωrt))
Which gives us
∣vr∣=2vsinωr
Hence the magnitude of the relative velocity will also have a time period of ω . Now since the magnitude of the relative velocity will always be positive, the negative values will be converted to positive values and in one time period, the relative velocity will peak twice.
So, the correct choice will be the option (A).
Note
In such questions, we must be aware of the basic concepts of angular velocity and how periodic objects change relative positions with time. The important distinction in the options is that the relative velocity can only peak twice in one time period of rotation which is the case with option (A) only because other options attain a maximum peak value at more than 2 points in a time period.
