Question

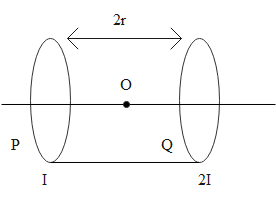
Two identical circular loops, P and Q, each of radius r and carrying currents I and 2I respectively are lying in parallel planes such that they have a common axis. The direction of current in both the loops is clockwise as seen from O which is equidistant from the both loops. Find the magnitude of the net magnetic field at point O.

Answer 1

This question is based on the concept of Biot-Savart law. Using the formula of the magnetic field along the perpendicular axis through the center of the coils P and Q, we will find the net magnetic field at point O.

Formula used:
$B=\dfrac{{{\mu }_{0}}I{{r}^{2}}}{2{{({{r}^{2}}+{{x}^{2}})}^{{}^{3}/{}_{2}}}}$

Complete step-by-step answer:
From the given question statement, we have the data as follows.
The radius of the loops P and Q, r
The distance from the center, 2r
The current through the loop P, I
The current through the loop Q, 2I

The expression of the magnetic field along the perpendicular axis through the center of the coil, that is, Biot-Savart law is given as follows.

$B=\dfrac{{{\mu }_{0}}I{{r}^{2}}}{2{{({{r}^{2}}+{{x}^{2}})}^{{}^{3}/{}_{2}}}}$
Where $I$is the current, $r$is the radius of the loop and $x$is the distance from the centre of the loop.
Firstly, we will find the expression for the magnetic field along the perpendicular axis through the center of the coil P. So, we have,

& {{B}_{P}}=\dfrac{{{\mu }_{0}}I{{r}^{2}}}{2{{({{r}^{2}}+{{r}^{2}})}^{{}^{3}/{}_{2}}}} \\\ & {{B}_{P}}=\dfrac{{{\mu }_{0}}I{{r}^{2}}}{2{{(2{{r}^{2}})}^{{}^{3}/{}_{2}}}} \\\ & {{B}_{P}}=\dfrac{{{\mu }_{0}}I{{r}^{2}}}{{{2}^{{}^{5}/{}_{2}}}{{r}^{3}}} \\\ \end{aligned}$$ Therefore, the expression for the magnetic field of the coil P is, $${{B}_{P}}=\dfrac{{{\mu }_{0}}I}{4\sqrt{2}r}$$. Secondly, we will find the expression for the magnetic field along the perpendicular axis through the center of the coil Q. So, we have, $$\begin{aligned} & {{B}_{Q}}=\dfrac{{{\mu }_{0}}(2I){{r}^{2}}}{2{{({{r}^{2}}+{{r}^{2}})}^{{}^{3}/{}_{2}}}} \\\ & {{B}_{Q}}=\dfrac{{{\mu }_{0}}2I{{r}^{2}}}{2{{(2{{r}^{2}})}^{{}^{3}/{}_{2}}}} \\\ & {{B}_{Q}}=\dfrac{{{\mu }_{0}}2I{{r}^{2}}}{{{2}^{{}^{5}/{}_{2}}}{{r}^{3}}} \\\ \end{aligned}$$ Therefore, the expression for the magnetic field of the coil Q is, $${{B}_{Q}}=\dfrac{{{\mu }_{0}}I}{2\sqrt{2}r}$$. The magnitude of the net magnetic field at point O is computed as follows. $$B={{B}_{P}}-{{B}_{Q}}$$ Substitute the obtained expressions of the magnetic fields of coils P and Q. $$B=\dfrac{{{\mu }_{0}}I}{4\sqrt{2}r}-\dfrac{{{\mu }_{0}}I}{2\sqrt{2}r}$$ Thus, the magnitude of the net magnetic field at point O is, $$B=\dfrac{{{\mu }_{0}}I}{4\sqrt{2}r}$$. $$\therefore $$ The magnitude of the net magnetic field at point O is, $$B=\dfrac{{{\mu }_{0}}I}{4\sqrt{2}r}$$. **Note:** The Biot-Savart law expression for computing the value of the magnetic field across the loop is the main concept to be used to find the magnitude of the net magnetic field at point O. The directions of the currents through the loops should be known.