Question

Two identical circular loops each of radius r carrying the same current I. These loops are concentric with their planes perpendicular to each other. Find the magnetic induction at their common centre.

Answer 1

Recall Right-hand rule to determine the direction of magnetic field produced by each loop at the common centre. Express the magnitude of the resultant magnetic field due to the magnetic field produced due to both the loops. Use the formula for magnetic field at the centre of the current carrying loop to calculate the magnetic field due to each loop separately.

Formula used:
$B = \dfrac{{{\mu _0}i}}{{2r}}$
Here, ${\mu _0}$ is the permeability of the free space, i is the current in the loop and r is the radius of the loop.

Complete Step by Step Answer:
We have given that the two circular loops are placed perpendicular to each other such that their centre coincides. We can draw the situation as shown in the figure below.

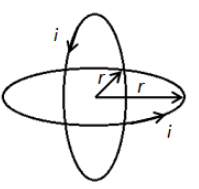
Due to the current in the loop, the magnetic field will be induced at the centre of the loop due to current in the both loops separately. Using the Right-hand thumb rule, we can denote the direction of the magnetic field at the centre of the loops as shown in the figure below.

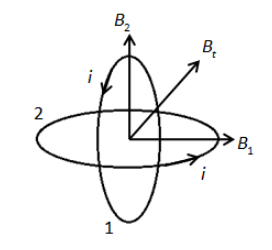
Thus, the magnetic fields due to loop 1 and loop 2 are perpendicular to each other as shown in the figure. The total magnetic field vector at the centre is,
${\vec B_t} = {\vec B_1} + {\vec B_2}$
In terms of magnitude, we can write the above equation as,
${B_t} = \sqrt {B_1^2 + B_2^2}$ …… (1)
We have the expression for the magnetic field at the centre of the circular loop,
$B = \dfrac{{{\mu _0}i}}{{2r}}$
Here, ${\mu _0}$ is the permeability of the free space, i is the current in the loop and r is the radius of the loop.

Since the current in the both loops is the same and the loops are identical, we can write,
${B_1} = {B_2} = \dfrac{{{\mu _0}i}}{{2r}}$
Using the above equation in equation (1), we get,
${B_t} = \sqrt {{{\left( {\dfrac{{{\mu _0}i}}{{2r}}} \right)}^2} + {{\left( {\dfrac{{{\mu _0}i}}{{2r}}} \right)}^2}}$
$\Rightarrow {B_t} = \sqrt {2{{\left( {\dfrac{{{\mu _0}i}}{{2r}}} \right)}^2}}$
$\Rightarrow {B_t} = \sqrt 2 \left( {\dfrac{{{\mu _0}i}}{{2r}}} \right)$
$\therefore {B_t} = \dfrac{{{\mu _0}i}}{{\sqrt 2 r}}$

This is the required expression for the magnetic field at the centre of the two circular loops placed perpendicular to each other.

Note: To answer this question, the thing that should be on your fingertips is the right-hand thumb rule. Remember, the direction of your thumb denotes the direction of current and curl fingers around the conductor denotes the direction of the magnetic field. We have assumed that the current in the both loops is counter clockwise.