Question

Two identical charged spheres suspended from a common point by two massless strings of length $l$ are initially a distance $d(d < < l)$ apart because of their mutual repulsion. The charge begins to leak from both the spheres at a constant rate. As a result the charges approach each other with a velocity $v$ . Then as a function of distance $x$ between them:
A) $v \propto {x^{ - 1/2}}$
B) $v \propto {x^{ - 1}}$
C) $v \propto {x^{1/2}}$
D) $v \propto x$

Answer 1

In order to solve this you have to draw a diagram first which shows the equilibrium positions of the two identical charged spheres that are suspended from a common point. Also indicate all the forces acting on two spheres and then apply the equilibrium conditions and write the equations.

Formula used:
The formula for coulombic force is given by
$F = \dfrac{{K{Q_1}{Q_2}}}{{{r^2}}}$
Where, $K$ is the proportionality constant and $K = \dfrac{1}{{4\pi {\varepsilon _0}}}$
${Q_1},{Q_2}$ are the charges
$r$ is the distance between the two charges

Complete step by step solution:

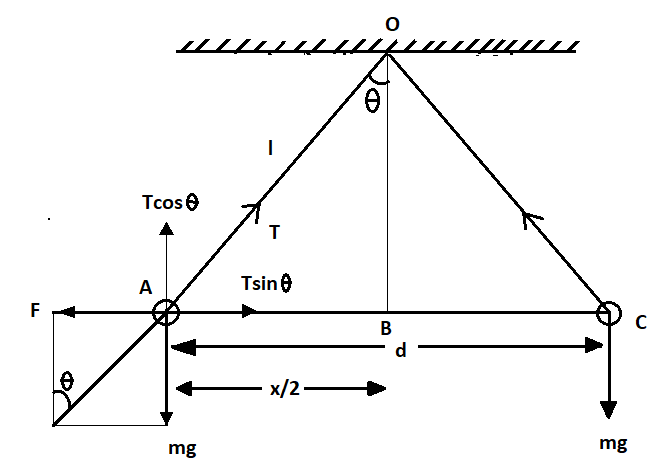
Here, in the above diagram there are two spheres A and C with identical charges $q$ and connected to a common point O at an angle of $\theta$ with a massless string of length $l$ and both the spheres are at a distance of $d$. The mass of both the spheres is given by $m$ due to which a gravitational force $mg$ acts downward on both the spheres and due to having identical charge a coulomb force $F$ is acted on both the spheres equal and opposite to each other. Let us assume the tension in the string is $T$.
Firstly break the components of tension force and then
By applying the equilibrium condition for sphere A, we get
$T\cos \theta = mg$ ………….(i)
And, $T\sin \theta = F$ ………….(ii)
Now, on dividing both the equations (i) and (ii), we get
$\Rightarrow$ $\tan \theta = \dfrac{F}{{mg}}$ …………(iii)
As we know that the coulomb force is given by,
$\Rightarrow$ $F = \dfrac{{K{Q_1}{Q_2}}}{{{r^2}}}$
Here given that the charge is same on both the spheres, that is $q$
On putting all the values, we get
$\Rightarrow$ $F = \dfrac{{K{q^2}}}{{{d^2}}}$
Now, put the above value in equation (iii), we get
$\therefore \tan \theta = \dfrac{{K{q^2}}}{{{d^2}mg}}$ ……….(iv)
It is given in the question that the charge begins to leak from both the spheres at a constant rate with a function of distance $x$ between them. Then the above equation becomes
$\Rightarrow \tan \theta = \dfrac{{K{q^2}}}{{{x^2}mg}}$
Now, from $\vartriangle AOB$, we have
$\Rightarrow$ $\tan \theta = \dfrac{{\dfrac{x}{2}}}{{\sqrt {{l^2} - \dfrac{{{x^2}}}{4}} }}$ ……….(v)
As $l > > x \Rightarrow {l^2} > > \dfrac{{{x^2}}}{4}$
So, neglect the term $\dfrac{{{x^2}}}{4}$.
Hence, ${l^2} - \dfrac{{{x^2}}}{4} \approx {l^2}$
Now, the equation (v) becomes,
$\Rightarrow$ $\tan \theta = \dfrac{x}{{2l}}$ …………(vi)
Now, from equation (iv) and (vi), we have
$\Rightarrow$ $\dfrac{x}{{2l}} = \dfrac{{K{q^2}}}{{{x^2}mg}}$
Now write the above equation in terms of x, we have
$\Rightarrow$ ${x^3} = \dfrac{{2K{q^2}l}}{{mg}}$
Here, all the terms are constant except $x$ and $q$
So, it is clear that,
$\Rightarrow$ ${x^3} \propto {q^2}$
On differentiating both sides with respect to time $t$, we get
$\Rightarrow$ $\dfrac{3}{2}{x^{1/2}}\dfrac{{dx}}{{dt}} \propto \dfrac{{dq}}{{dt}}$
Here, $\dfrac{{dx}}{{dt}}$ is the rate of change of distance, which is known as velocity. So, the charges approach each other with a velocity $v$.
Hence, $\dfrac{{dx}}{{dt}} = v$ and $\dfrac{{dq}}{{dt}} =$ constant
So, our above equation becomes
$\Rightarrow$ $v \propto {x^{ - 1/2}}$

Therefore, the correct option is (A).

Note: Remember that when two charges separated by a distance ${r_0}$ in a vacuum and the force between them is same as the force between the same charges separated by a distance $r$ in a medium, then from Coulomb’s Law; $K{r^2} = {r_0}^2$. Also remember that the coulomb’s law is only applicable for the point charges at rest.