Question

Two identical charged spheres suspended from a common point by two massless strings of lengths $l$ , are initially at a distance $d\;(d \ll l)$ apart because of their mutual repulsion. The charges begin to leak from both the spheres at a constant rate. As a result, the spheres approach each other with a velocity $v$ . Then $v$ varies as a function of the distance $x$ between the spheres, as:
A) $v \propto {x^{\dfrac{1}{2}}}$
B) $v \propto x$
C) $v \propto {x^{ - \dfrac{1}{2}}}$
D) $v \propto {x^{ - 1}}$

Answer 1

Hint : In this solution, we will find the angle made by the charged particles with the normal and determine the relationship between the distance between the spheres and the charge of the spheres. We will then differentiate the charge of the spheres to determine the relation of the distance between the spheres as a function of the velocity of the particles.

Formula used: In this question, we will use the following formula
$\Rightarrow F = \dfrac{{k{Q^2}}}{{{x^2}}}$ where $F$ is the force between two identical charged objects having charge $Q$ and distance $x$ between them

Complete step by step answer
We’ve been given that the two identical charged spheres suspended from a common are initially at a distance $d\;(d \ll l)$ and then the charges begin to leak from both the spheres at a constant rate. Before starting the solution, let us draw a diagram of the scenario:

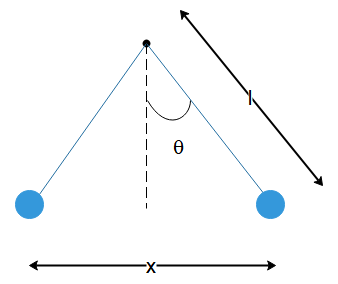
In the diagram given above, the angle $\theta$ is very small as $(d \ll l)$ . So we can say that $\tan \theta \approx \sin \theta$
So, we can see that the tangent of the angle $\theta$ can be written as $\tan \theta \approx \sin \theta = \dfrac{{x/2}}{l}$ since $x/2$ is the distance between the particles and the normal to the surface and $l$ is the length of the string.
Now, for the tension in the string, we can write the components of tension in the string as
$\Rightarrow T\cos \theta = mg$
And
$\Rightarrow T\sin \theta = F$ where $F = \dfrac{{k{Q^2}}}{{{x^2}}}$
Taking the ratio of equation (2) by equation (1), we get
$\Rightarrow \tan \theta = \dfrac{F}{{mg}}$
But since $\tan \theta = \dfrac{{x/2}}{l}$ , we can write
$\Rightarrow \dfrac{F}{{mg}} = \dfrac{x}{{2l}}$
$\Rightarrow \dfrac{{k{Q^2}}}{{mg{x^2}}} = \dfrac{x}{{2l}}$
To determine the relation of the distance between the charged objects, since the charge of the objects is leaking, we only need the relation between $x$ and $Q$ so we can write
$\Rightarrow {x^3} \propto {Q^2}$
$\Rightarrow {x^{3/2}} \propto Q$
Then to calculate the velocity of the charges, we will differentiate both sides of the above equation.
$\Rightarrow 3{x^2}\dfrac{{dx}}{{dt}} \propto 2Q\dfrac{{dQ}}{{dt}}$ where $\dfrac{{dQ}}{{dt}}$ is constant as the charge leaks at a constant rate.
As $dx/dt = v$ , we can write
$\Rightarrow 3{x^2}v \propto 2Q$
Again as ${x^{3/2}} \propto Q$ , we can write
$\Rightarrow 3{x^2}v \propto 2{x^{3/2}}$
$\therefore v \propto {x^{ - 1/2}}$
Which corresponds to option (C).

Note
The small-angle approximation that we used at the beginning of the solution is only valid if $(d \ll l)$ . Otherwise, we wouldn’t be able to approximate $\tan \theta \approx \sin \theta$ which simplifies our solution.