Question

Two identical charged spheres suspended from a common point by two massless strings of lengths $l$, are initially at a distance $d(d << l)$ apart because of their mutual repulsion. The charges begin to leak from both the spheres at a constant rate. As a result, the spheres approach each other with a velocity $v$. Then $v$ varies as a function of the distance $x$ between the spheres, as:
a) $v$ ${{x}^{1/2}}$
b) $v$ ${{x}^{{}}}$
c) $v$ ${{x}^{-1/2}}$
d) $v$ ${{x}^{-1}}$

Answer 1

The two spheres exert an electric force of $F$ on each other. This force is directed away from each other. Gravitational force acts vertically downwards. Also, the movement of the ball is in the direction opposite to the direction of electric force $F$.
Formula Used:
$\tan \theta =\dfrac{F}{mg}$
$F=\dfrac{k{{q}^{2}}}{{{x}^{2}}}$

Complete answer:
Here, consider two spheres with charges $q$ each suspended from a common point with the help of two different strings of each length $l$. Due to similar charge, let them be initially separated by a distance d from each other. This can be pictorially depicted as follows:

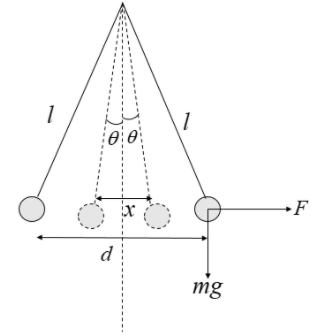
Here, let the force acting on the two spheres due to the other sphere be $F$. Here, the forces are acting on the bodies as shown on the diagram.
Here, we know that the relation between the force $F$ and the weight $mg$ is given as:
$\tan \theta =\dfrac{F}{mg}$ -------(i)
We know that $d<Also, for small angle$\theta $, we can know:$\tan \theta \simeq \theta $Hence in the equation (i)$\tan \theta =\dfrac{F}{mg}\simeq \theta $------(ii) Here, we can write$\tan \theta $as:$\tan \theta =\dfrac{(x/2)}{l}=\dfrac{x}{2l}$$\Rightarrow \theta =\dfrac{x}{2l}$Using equation (ii)$\dfrac{F}{mg}=\dfrac{x}{2l}$Also, we know that the force acting on the charged sphere due to another charged sphere hanged in front of the other as shown in the diagram is given by:$F=\dfrac{k{{q}^{2}}}{{{x}^{2}}}$-----(iii) Putting equation (iii) in the above equation, we get:$\dfrac{k{{q}^{2}}}{{{x}^{2}}mg}=\dfrac{x}{2l}$Here apart from$x$and$q$rest all the parameters are constant. Hence, we can re-write this equation as:${{x}^{3}}=K{{q}^{2}}$--------(iv)$\Rightarrow q={{K}{1}}{{x}^{3/2}}$-------(v) Thus we can say that the cube of the separation distance varies with the square of the charge on the body of the sphere. Also, we can further simplify the equation (iv) as, differentiating both sides with respect to$t$, we get:$\dfrac{d}{dt}({{x}^{3}})=K\dfrac{d}{dt}{{(q)}^{2}}$$3{{x}^{2}}\dfrac{dx}{dt}=2Kq\dfrac{dq}{dt}$Here,$\dfrac{dx}{dt}$is nothing but the speed. Hence we can replace it as:$3{{x}^{2}}v=2Kq\dfrac{dq}{dt}$Now, according to question, charges leak from both the spheres at a constant rate. This implies that$\dfrac{dq}{dt}$is constant. Hence, we can write:${{x}^{2}}v={{K}{2}}q$Replacing the value of$q$using equation (v), we get:${{x}^{2}}v={{K}{2}}{{K}{1}}{{x}^{3/2}}$$\Rightarrow v={{K}_{3}}{{x}^{-1/2}}$This can also be written as:$v$$\propto$${{x}^{-1/2}}$

Hence, option (c) is the correct answer.

Note:
Note carefully that $x$ is a random distance between the two spheres at any random point of time. This is spread over in both the regions separated by the dotted line. Hence, while taking $\tan \theta$, we took $\dfrac{x}{2}$, rather than taking only $x$ as the perpendicular to be put in $\tan \theta$.