Question

Two identical charged spheres suspended from a common point by two massless strings of length $\ell$ are initially a distance $d(d < < \ell )$ apart because of their mutual repulsion. The charge begins to leak from both spheres at a constant rate. As a result the charges approach each other with a velocity v. Then as a function of distance x between them
(A) $v \propto {x^{ - 1/2}}$
(B) $v \propto {x^{ - 1}}$
(C) $v \propto {x^{1/2}}$
(D) $v \propto x$

Answer 1

If 2 identical charged particles are suspended from a common point like pendulum then in equilibrium the balancing conditions of forces is given as
$T\sin \theta = {F_e} = \dfrac{{k{q_1}{q_2}}}{{{r^2}}} = \dfrac{{k{q^2}}}{{{r^2}}}$
$T\cos \theta = mg$
Where q is the charge of a particle and m is the mass of the particle.

Complete step by step answer:
Here, given that 2 charges (identical) are suspended from a common point by 2 massless strings of length $\ell$ and initial distance between them is d. So, from diagram, we can easily balance the forces

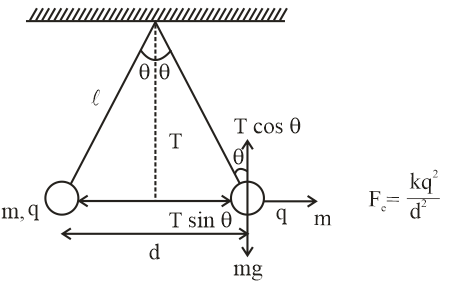
So, in equilibrium
$T\cos \theta = mg$ …..(1)
$T\sin \theta = {F_e} = \dfrac{{k{q^2}}}{{{d^2}}}$ …..(2)
From equation $2/1$
$\tan \theta = \dfrac{{T\sin \theta }}{{T\cos \theta }} = \dfrac{{{F_e}}}{{mg}}$ ….(3)
Now, charge begins to leak from both the spheres, then equation 3 becomes
$\tan \theta = \dfrac{{{F_e}}}{{mg}} = \dfrac{{k{q^2}}}{{{x^2}mg}}$ …..(4)
From diagram we can write
$\tan \theta = \dfrac{{x/2}}{\ell } = \dfrac{x}{{2\ell }}$ …..(5)

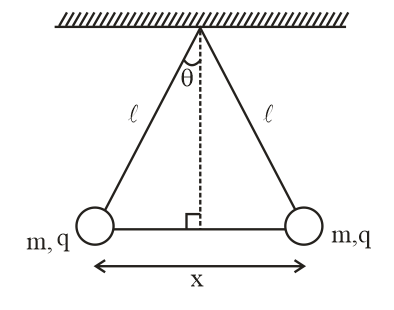
So, from equation 4 & 5
$\dfrac{{k{q^2}}}{{{x^2}mg}} = \dfrac{x}{{2\ell }}$
Here k, m, g and $\ell$ are constants (fixed)
So, ${x^3} \propto {q^2}$ …..(6)
On differentiating the above equation w.r.t. time t we get
$3{x^2}\dfrac{{dx}}{{dt}} \propto 2q\dfrac{{dq}}{{dt}}$
Given that rate of leakage of charge is constant i.e., $\dfrac{{dq}}{{dt}} = cons\tan t$
$3{x^2}\dfrac{{dx}}{{dt}} \propto 2q$
$\because \dfrac{{dx}}{{dt}} = v$ [3 & 2 are also constant]
So, ${x^2}(v) \propto q$ …(7)
From equation 6
$\because 3{x^3} \propto {q^2}$
$\therefore {x^{3/2}} \propto q$ …..(8)
From equation 7 & 8
${x^2}(v) \propto {x^{3/2}}$
$v \propto \dfrac{{{x^{3/2}}}}{{{x^2}}} \Rightarrow v \propto {x^{3/2}}{x^{ - 2}}$
$v \propto {3^{3/2 - 2}} \Rightarrow v \propto {x^{ - 1/2}}$

So, the correct answer is “Option A”.

Note:
In many problems, charges are not identical. In that case masses will be compared by equation $T\cos \theta = mg$ and when charges are different then problems will be solved by equation
$T\sin \theta = {F_e} = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$