Question

Two identical charged spheres suspended from a common point by two massless strings of length l are initially a distance d (d << l) apart because of their mutual repulsion. The charge begins to leak from both the spheres at a constant rate. As a result the charges approach each other with a velocity v. Then as a function of distance x between them:

& A.\,v\propto {{x}^{-1/2}} \\\ & B.\,v\propto {{x}^{-1}} \\\ & C.\,v\propto {{x}^{1/2}} \\\ & D.\,v\propto x \\\ \end{aligned}$$

Answer 1

It becomes easy to solve this question using a free body diagram of the spheres suspended from a common point by two massless strings of length and initially a distance apart. We will be equating the horizontal forces to find the expression of the velocity in terms of the distance.
Formula used:
$F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}^{2}}}{{{d}^{2}}}$

Complete answer:
From the given information, we have the data as follows.
Two identical charged spheres suspended from a common point by two massless strings of length l are initially a distance d (d << l) apart because of their mutual repulsion. The charge begins to leak from both the spheres at a constant rate.
Consider the free body diagram of spheres.

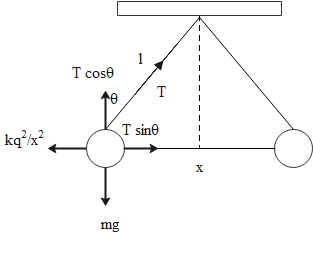
From the above figure, it’s clear that,
$T\sin \theta =\dfrac{k{{q}^{2}}}{{{x}^{2}}}$ …… (1)
$T\cos \theta =mg$…… (2)
Divide the equations (1) and (2).

& \tan \theta =\dfrac{{}^{k{{q}^{2}}}/{}_{{{x}^{2}}}}{mg} \\\ & \Rightarrow \tan \theta =\dfrac{k{{q}^{2}}}{{{x}^{2}}mg} \\\ \end{aligned}$$ Here $$\tan \theta \approx \theta $$, so, $$\theta =\dfrac{k{{q}^{2}}}{{{x}^{2}}mg}$$ Again, we have, $$\dfrac{x}{2l}=\dfrac{k{{q}^{2}}}{{{x}^{2}}mg}$$ $$\begin{aligned} & \Rightarrow {{q}^{2}}=\dfrac{mg{{x}^{3}}}{2kl} \\\ & \Rightarrow q={{\left( \dfrac{mg{{x}^{3}}}{2kl} \right)}^{{1}/{2}\;}} \\\ \end{aligned}$$ The rate of charge leakage equals ‘r’. $$\begin{aligned} & \therefore \dfrac{dq}{dt}=r \\\ & \Rightarrow \dfrac{dq}{dt}=c\times \dfrac{3}{2}{{x}^{{1}/{2}\;}}\dfrac{dx}{dt}\,\,\,\,\,\,\,\,\,\,\,\left( \dfrac{dx}{dt}=v \right) \\\ & \therefore r=c\sqrt{x}\dfrac{dx}{dt} \\\ & \Rightarrow \dfrac{dx}{dt}=k{{x}^{-1/2}} \\\ & \therefore v\propto \dfrac{1}{\sqrt{x}} \\\ \end{aligned}$$ Or, we can continue the computation as, $$\begin{aligned} & \Rightarrow q\propto {{c}^{{}^{3}/{}_{2}}} \\\ & \Rightarrow \dfrac{dq}{dt}\propto \dfrac{3}{2}{{x}^{1/2}}\left( \dfrac{dx}{dt} \right) \\\ & \therefore \dfrac{dx}{dt}\propto {{x}^{-1/2}} \\\ \end{aligned}$$ We can solve this problem directly as follows. We can consider the equation (1) as follows. $$\begin{aligned} & T\sin \theta =F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}^{2}}}{{{d}^{2}}} \\\ & \tan \theta =\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}^{2}}}{{{x}^{2}}mg} \\\ \end{aligned}$$ Now substitute the expression of the tan of angle as $$\tan \theta =\dfrac{x}{2l}$$in the above equation. $$\begin{aligned} & \Rightarrow \dfrac{x}{2l}\propto \dfrac{{{q}^{2}}}{{{x}^{2}}} \\\ & \Rightarrow {{q}^{2}}\propto {{x}^{3}} \\\ & \therefore q\propto {{x}^{3/2}} \\\ \end{aligned}$$ (as the length is constant value, so, we get a proportionality equation) Differentiate the above equation. So, we get, $$\dfrac{dq}{dt}\propto \dfrac{3}{2}{{x}^{1/2}}\dfrac{dx}{dt}$$ Again here $$\dfrac{dx}{dt}$$is constant. $$\begin{aligned} & \dfrac{dq}{dt}\propto \dfrac{3}{2}{{x}^{1/2}}\dfrac{dx}{dt} \\\ & \Rightarrow v\propto {{x}^{-1/2}} \\\ \end{aligned}$$ $$\therefore $$The velocity in terms of the distance is $$v\propto {{x}^{-1/2}}$$ **Thus, option (A) is correct.** **Note:** The relation between the velocity and the distance is a derivation formula. We should know that the rate of charge leakage is constant and the velocity is constant to continue the computation.