Question

Two identical charged spheres are suspended by strings of equal length. The strings make an angle of $30{\circ}$ with each other. When suspended in a medium of density$0.8 g \ cm^{-3}$, the angle remains the same. If the density of the material of the sphere is $1.6 g \ cm^{-3}$, the dielectric constant of the liquid is:
A. 4
B. 3
C. 2
D. 1

Answer 1

In the system, major forces are electrostatic and tension. But when a body is suspended into a different medium, an additional force of buoyancy starts acting on to it. This force will act upwards and hence should increase the angular separation between them. But this is not the case. The angle still remains the same. The reason behind it is the reduction of electrostatic forces.

Complete step-by-step solution:
We know that if charges are placed in a medium that has different dielectric constant that free space, the force of electrostatic gets reduced by a factor called it’s dielectric constant. Let the dielectric constant of the medium in the above question be ‘s’.
Now we’ll derive the expression for the angle subtended by the charges.

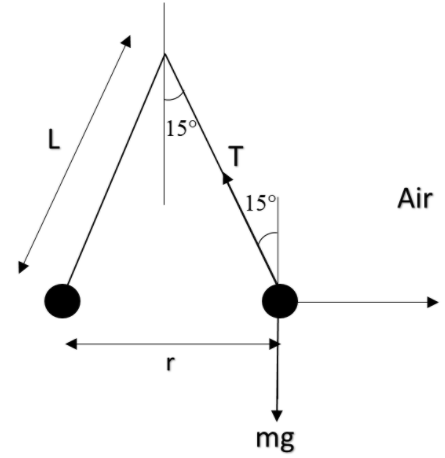
Drawing FBD of the sphere for air:

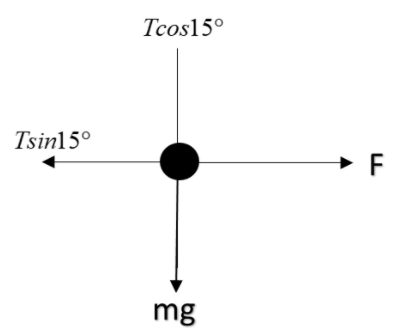
Now, for being in equilibrium, forces along y and x-axis must be zero.
In ‘x’ direction:
F=T sin15 .......................…..①
In ‘y’ direction:
mg= T cos15 ..................…..②
Now, dividing equation ① and ② we get;
$\dfrac{F}{mg} = \dfrac{T \sin 15^\circ}{T \cos 15^\circ} = \tan 15^\circ$ ...................③
Now, if the spheres are placed in the liquid:
Let the mass of the sphere = m.

Drawing FBD for the medium:

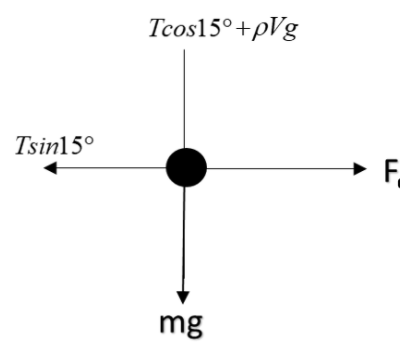
Now, for being in equilibrium, forces along y and x-axis must be zero.
In ‘x’ direction:
$F_1=T \sin 15^\circ$ ……......…..④
In ‘y’ direction:
$mg - \rho Vg = T \cos15^\circ$ .................…..⑤
Now dividing ④ and ⑤, we get;
$\dfrac{F_1}{mg - \rho Vg} = \dfrac{T \sin 15^\circ}{T \cos15^\circ} =\tan 15^\circ$
Now, putting the value of tan 15 from ③, we get
$\dfrac{F}{mg}= \dfrac{F_1}{mg-\rho Vg}$
Now, as we know if the dielectric constant of the medium is ‘s’, then the electrostatic force will reduce by the factor ‘s’ Hence, $F_1 = \dfrac Fs$
Also putting mass (m) = $\sigma V$, where $\sigma$ is the density of sphere.
$\dfrac{F}{\sigma Vg}= \dfrac{\dfrac Fs}{\sigma Vg-\rho Vg}$
$\dfrac{1}{\sigma }= \dfrac{\dfrac 1s}{\sigma -\rho }$
Hence $s = \dfrac{\sigma}{\sigma - \rho}$
On putting the values,
$s=\dfrac{1.6}{1.6-0.8}=\dfrac{1.6}{0.8} = 2$
Thus the dielectric constant of the medium is 2, option C is correct.

Note: Permittivity of a medium is the measure of resistance towards the formation of electric field. The charges experience the maximum force when placed in free space. In the case of any other medium, the force gets reduced by a factor called the dielectric constant of the medium which is a unique property of the medium.