Question
Question: Two identical capacitors A and B, charged to the same potential V are connected in two different cir...
Two identical capacitors A and B, charged to the same potential V are connected in two different circuits as shown below at time t=0. If the charge on capacitors A and B at time t=CR is QA and QB respectively, then (Here e is the base of natural logarithm)
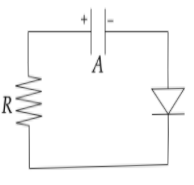
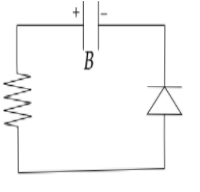
(A)QA=VC,QB=eVC
(B)QA=2CV,QB=eVC
(C)QA=VC,QB=CV
(D)QA=eVC,QB=2CV
Solution
Analyzing both the circuits we can solve the problem. In the first case the diode is reversed biased while in the second case the diode will act as a forward case. Now using reverse biased and forward biased concepts respectively in the above to find the charge flows through the circuit using charge voltage and capacitance relation.
Complete step by step answer:
As per the problem we have two identical capacitors A and B, charged to the same potential V are connected in two different circuits as shown below at time t=0. If the charge on capacitors A and B at time t=CR is QA and QB respectively.
We need to calculate the charge in both cases.
Let us first take the first case:
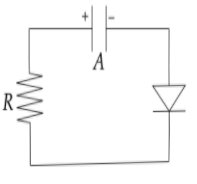
Here we can see that the negative terminal of the diode is connected to the negative terminal of the capacitor hence it is a reversed biased diode due to which no current will flow through it. So, there will be no current in the circuit, the charge on the capacitor will remain the same always.
Now,
Potential of the capacitor = V
Capacitance of the capacitor = C
Charge of the capacitor = Q
Now those charges will remain the same.
So charge on A will be,
QA=CV
Let us first take the second case:
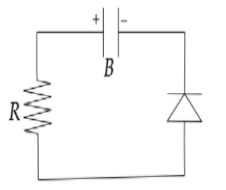
Here we can see that the positive terminal of the diode is connected to the negative terminal of the capacitor hence it is a forward biased diode due to which it acts as a closed circuit. So the charge in the capacitor starts decaying after some time t. Now,
Q=CV
Q will change to QB after some time t.
So charge on B will be,
QB=QeRC−t
Potential of the capacitor = V
Capacitance of the capacitor = C
Charge of the capacitor = Q
The base of natural logarithm = e
Now at time t=CR we will get charge equal to,
QB=QeRC−CR
On cancelling the terms we will get,
QB=Qe−1
Now putting Q value in the above equation we will get,
QB=eCV
Therefore the above equation we will get (A).
Note: The decay of charge in a capacitor is similar to the decay of the radioactive nuclide and it is an exponential expression or we can say it as exponential decay. Remember that the voltage, current and charge all will decay exponentially during the capacitor discharge. In case of reversed biased the circuit will act as an open circuit while in case of forward biased the circuit will act as a closed circuit.
