Question
Question: Two identical billiard balls strike a rigid wall with the same speed but at different angles, and ge...
Two identical billiard balls strike a rigid wall with the same speed but at different angles, and get reflected without any loss of speed, as shown in the figure. What is (i) the direction of the force of the wall due to each ball? And (ii) the ratio of the magnitudes of the impulses imparted on the two balls by the wall?
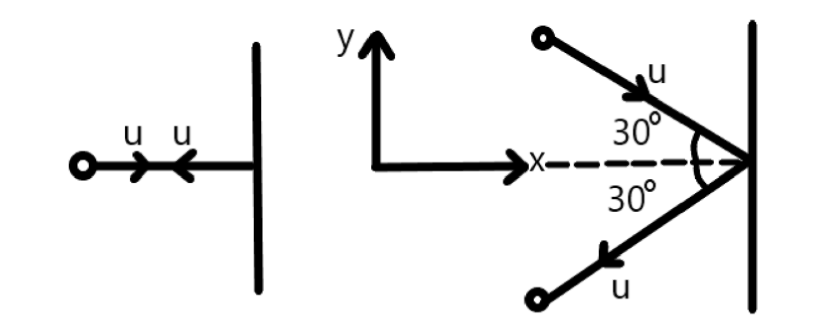
Solution
Impulse is defined as the amount of force that is applied on an object for a certain amount of time that causes a change in momentum. Here, we will first change in velocity of the first ball to calculate the impulse of both the balls. Here, the direction of the force will be equal to the direction of momentum.
Complete step by step solution:
Consider that two balls are sticking against the ball with the same speed but at the different angles.Therefore, let the angle of incidence of the first ball on the wall is =A
Also, let the angle of incidence of the second ball on the wall is =B
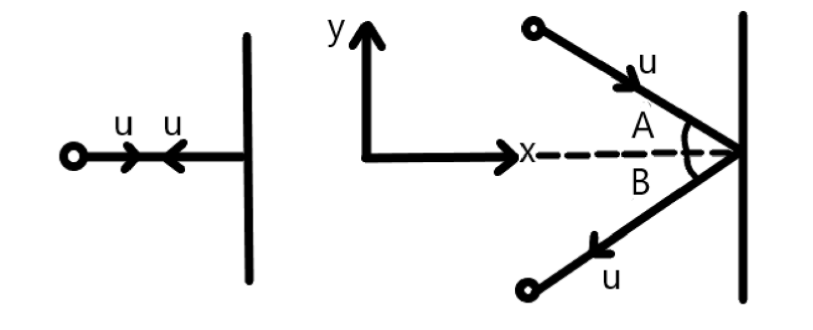
Now, let the speed of the balls before striking the wall =V
Now, let us resolve the velocity vectors (incident and reflected) into two parts that will be vcosA along the normal to the wall and vsinA along the wall.
Now, the change in the velocity of the first ball =vf−vi
⇒(vcosAj+vsinAi)−(vsinAi−vcosA)
⇒2vcosAj
Now, we know that impulse is equal to the change in momentum. As we know that, momentum is given by
p=mv
⇒p=2mvcosAj
Therefore, impulse =2mvcosAj
Hence, the direction of the force will be equal to the direction of momentum which will be equal to the normal of the wall.
Now, the ratio of the impulse =IBIA
⇒2mvcosB2mvcosA
⇒cosBcosA
Therefore, we can say that the ratio of the impulses is equal to the ratio of the cosines of the angle of incidence.
Note:
Here, we have not taken the angle of the balls made with the ball as 30∘ , but if we put the value of the angle, the ratio of the impulse will become
The ratio of the impulse =cosBcosA
⇒cos30∘cos30∘
⇒1
Therefore, from the above value, we can say that the impulse of the ball A will be equal to the impulse of the ball B.
