Question

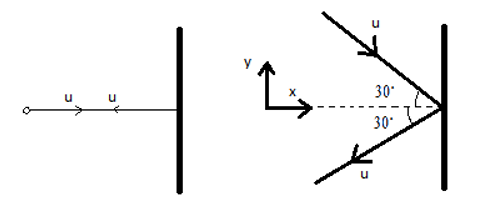
Two identical billiard balls strike a rigid wall with the same speed but at different angles, and get reflected without any loss of speed as shown in the figure. What is $\left( i \right)$ the direction of the force of the wall due to each ball? And $\left( ii \right)$ the ratio of magnitudes of the impulses imparted on the two balls by the wall?

Answer 1

To solve the parts of the given question, the concept of impulse must be thorough. Impulse of a force is the total effect of a large force which acts for a short time to produce a finite change in momentum and is physically the integral of a force over the time interval.

Complete step by step answer:
Primarily, to find the direction of the force of the wall due to each ball,
Let $u$ be the speed of each ball before and after collision with the wall, and $m$ be the mass of each ball and then choose the $y-axis$ and $x-axis$ as given in the above picture.
In according to the question,
In x component,
Initial momentum,$p_{x}^{initial}=mu$ and final momentum $p_{x}^{final}=-mu$
In y component,
Initial momentum,$p_{y}^{initial}=0$ and final momentum $p_{y}^{final}=0$
As $impulse=change\text{ }in\text{ }momentum$
Therefore, $x-component of\text{ }the\text{ }impulse=-mu-mu=-2mu$
And $y-components of\text{ }the\text{ }impulse=0$
It is clear that the direction of the impulse is along the negative $x-$direction of the motion and as the direction of the force is the same as that of impulse, so the force on the ball due to the wall is normal to the wall and along the $x-$direction of the motion. Thus by Newton’s third law of motion, the force on the wall due to the ball is normal to the wall along the positive $x-$direction of the motion.
Now, for the second ball incident at the wall at ${{30}^{\circ }}$
In x component,
Initial momentum,$p_{x}^{initial}=mu\cos {{30}^{\circ }}$ and final momentum $p_{x}^{final}=-mu\cos {{30}^{\circ }}$
In y component,
Initial momentum,$p_{y}^{initial}=-mu\sin {{30}^{\circ }}$ and final momentum $p_{y}^{final}=-mu\sin {{30}^{\circ }}$
Therefore, $x-component\ of\text{ }the\text{ }impulse=-mu\cos {{30}^{\circ }}-mu\cos {{30}^{\circ }}=-2mu\cos {{30}^{\circ }}$
And $y-components\ of\text{ }the\text{ }impulse=-mu\sin {{30}^{\circ }}+mu\sin {{30}^{\circ }}=0$
Again, the direction of the impulse is normal to the wall along the negative $x-$direction and by Newton’s third law of motion, the force on the wall due to the ball is normal to the wall along the positive $x-$direction.
Secondarily, we need to find the ratio of magnitudes of the impulses imparted on the two balls by the wall; we need to find the ratio of magnitudes of $x-component of\text{ }$ the impulse imparted on the two balls by the wall i.e.
${{p}_{a}}:{{p}_{b}}=-2mu:-mu\cos {{30}^{\circ }}$
$\Rightarrow {{p}_{a}}:{{p}_{b}}=-2:\frac{\sqrt{3}}{2}$
$\Rightarrow {{p}_{a}}:{{p}_{b}}=4:\sqrt{3}$

Therefore the ratio of the impulses imparted on the two balls by the wall is $4:\sqrt{3}$.

Note:
One is advised to carefully observe that only the $y-component\ of\text{ }$ impulse imparted on the two balls due to the wall while calculating the ratio of magnitudes of the impulses imparted on the two balls by the wall as the $y-component of\text{ }$ the impulse is null in both the cases.