Solveeit Logo
Login

Question

Question: Two identical billiard balls of diameter 5 cm, each moving with a speed of 3 m $s^{-1}$, roll, witho...

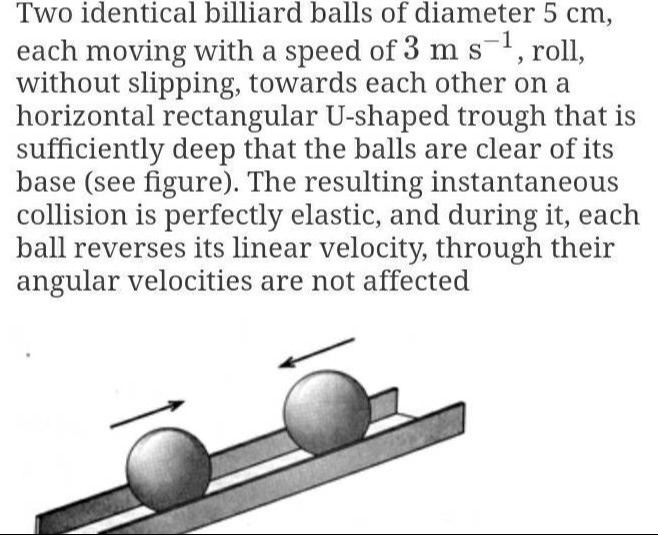
Two identical billiard balls of diameter 5 cm, each moving with a speed of 3 m s−1s^{-1}, roll, without slipping, towards each other on a horizontal rectangular U-shaped trough that is sufficiently deep that the balls are clear of its base (see figure). The resulting instantaneous collision is perfectly elastic, and during it, each ball reverses its linear velocity, through their angular velocities are not affected

Answer

The balls are slipping after the collision.

Explanation

Solution

The problem describes a collision between two identical billiard balls rolling without slipping.

Initial state:

Diameter = 5 cm, so radius R=2.5R = 2.5 cm =0.025= 0.025 m. Speed of each ball = 3 m/s. Let the initial velocity of the first ball be v1=3v_1 = 3 m/s and the initial velocity of the second ball be v2=−3v_2 = -3 m/s. Since the balls are rolling without slipping, the initial angular velocities are ω1=v1/R=3/0.025=120\omega_1 = v_1/R = 3/0.025 = 120 rad/s and ω2=v2/R=−3/0.025=−120\omega_2 = v_2/R = -3/0.025 = -120 rad/s.

Collision:

The collision is perfectly elastic. Each ball reverses its linear velocity. So, the final linear velocities are v1′=−v1=−3v_1' = -v_1 = -3 m/s and v2′=−v2=3v_2' = -v_2 = 3 m/s. Their angular velocities are not affected. So, the final angular velocities are ω1′=ω1=120\omega_1' = \omega_1 = 120 rad/s and ω2′=ω2=−120\omega_2' = \omega_2 = -120 rad/s.

Let's check if the balls are rolling without slipping after the collision. For rolling without slipping, the condition is v′=Rω′v' = R\omega'. For the first ball: v1′=−3v_1' = -3 m/s, Rω1′=0.025×120=3R\omega_1' = 0.025 \times 120 = 3 m/s. Since v1′≠Rω1′v_1' \neq R\omega_1', the first ball is slipping after the collision. Specifically, v1′=−Rω1′v_1' = -R\omega_1'. For the second ball: v2′=3v_2' = 3 m/s, Rω2′=0.025×(−120)=−3R\omega_2' = 0.025 \times (-120) = -3 m/s. Since v2′≠Rω2′v_2' \neq R\omega_2', the second ball is slipping after the collision. Specifically, v2′=−Rω2′v_2' = -R\omega_2'.

Explanation of the solution:

  1. Identify the initial linear and angular velocities using the given speed and the rolling without slipping condition (v=Rωv = R\omega).
  2. Use the given information about the collision to find the final linear and angular velocities. The linear velocity is reversed, and the angular velocity is unchanged.
  3. Check the condition for rolling without slipping (v′=Rω′v' = R\omega') for the final state of each ball.
  4. Compare v′v' and Rω′R\omega' for each ball after the collision. If they are not equal, the ball is slipping.