Question

Two identical beakers A and B contain equal volumes of two different liquids at $60^{\circ}$ each and left to cool down. Liquid in A has density $8\times 10^{2} kgm^{-3}$ and specific heat $2000 J\;kg^{-1}\;K^{-1}$ while liquid B has density $10^{3} kgm^{-3}$ and specific heat $4000 J\;kg^{-1}\;K^{-1}$. Which of the following best describes their temperature versus time graph schematically? (Assume the emissivity of both the beakers to be the same).
A.

B.

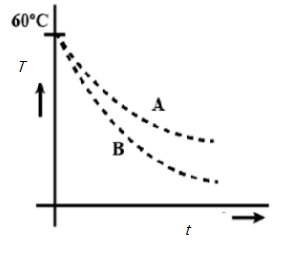
C.

D.

Answer 1

Newton’s laws of cooling states that the rate of heat loss of a body is directly proportional to the difference in the temperature between the body and its surroundings. We can solve the problem by using Newton’s law of cooling and the first law of thermodynamics.

Formula used:
$\dfrac{dU}{dt}=C\dfrac{dT}{dt}$
$\dfrac{dT}{dt}=\dfrac{ Q}{(\rho\times v)\times c}$

Complete step by step answer:
Newton’s laws of cooling states that the rate of heat loss of a body is directly proportional to the difference in the temperature between the body and its surroundings.
He also noted that, with some mathematical manipulation of the law, he found that the rate of temperature change of a body is proportional to the difference in temperatures between the body and its surroundings . This was done to override the confusion in Newton's time between the concepts of heat and temperature.
He gave that $C=\dfrac{dU}{dT}$, where $C$ is the heat capacitance, $U$ is the internal energy of the system, and $T$ is the temperature.
Differentiating $U$ wrt time $t$, we get
$\dfrac{dU}{dt}=C\dfrac{dT}{dt}$
We know that, $C= mc$ and $m=\rho\times v$ , where $m$ is mass of the substance, $\rho$ is density and $v$ is volume of the substance and $c$ is specific heat of the substance.
Also, from the first law of thermodynamics $dv{U}{t}=-Q$ i.e. loss of heat energy to the surroundings. Since both A & B beakers are left to cool in the same conditions, $Q$ is the same for both the beakers.
Then $Q=(\rho\times v)\times c\dfrac{dT}{dt}$
$\dfrac{dT}{dt}=\dfrac{ Q}{(\rho\times v)\times c}$
Since volume and loss of heat is same for both the beakers
$\dfrac{dT}{dt}=\dfrac{k}{\rho\times c}\;; k=\dfrac{Q}{v}$
For $\dfrac{A}{B}=\dfrac{\dfrac{dT_{1}}{dt}}{\dfrac{dT_{2}}{dt}}=\dfrac{\rho_{2}c_{2}}{\rho_{1}c_{1}}$ given$\rho_{1}=8\times 10^{2} kgm^{-3}\;;c_{1}=2000 J\;kg^{-1}\;K^{-1}\;\rho_{2}=10^{3} kgm^{-3}\;;c_{2}=4000 J\;kg^{-1}\;K^{-1}$
$\dfrac{A}{B}=\dfrac{\dfrac{dT_{1}}{dt}}{\dfrac{dT_{2}}{dt}}=\dfrac{10^{3} \times 4000 }{8\times 10^{2} \times2000}=\dfrac{4\times10^{6}}{16\times10^{5}}$
Means $\dfrac{dT_{1}}{dt}>\dfrac{dT_{2}}{dt}$

Hence A is the answer.

Note:
Be careful in interpreting the results graphically. Be careful with the symbols and notations used. Try to remember the principle and the formulas used. Remember that the law is converted into two forms.