Question

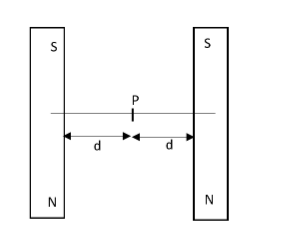
Two identical bar magnets each of it having magnetic moment $M$ are placed as shown in the figure. The magnetic field at point P will be given as,

$\begin{aligned} & A.2\left( \dfrac{{{\mu }_{0}}}{4\pi } \right)\dfrac{M}{{{d}^{3}}} \\\ & B.\left( \dfrac{{{\mu }_{0}}}{4\pi } \right)\dfrac{M}{{{d}^{3}}} \\\ & C.\sqrt{5}\left( \dfrac{{{\mu }_{0}}}{4\pi } \right)\dfrac{M}{{{d}^{3}}} \\\ & D.2\sqrt{5}\left( \dfrac{{{\mu }_{0}}}{4\pi } \right)\dfrac{M}{{{d}^{3}}} \\\ \end{aligned}$

Answer 1

Magnetic field due to the bar magnet is given by taking the product of the ratio of the magnetic permeability to the constant $4\pi$ and the ratio of the magnetic moment of the Bar magnet to the distance between the points. This should be calculated for each of the bar magnets and find out the answer. Hope these all may help you to solve this question.

Complete answer:
Let us mention what all are given in the question first of all. The magnetic moment of each of the magnets is given by $M$, the point at which the magnetic field is to be calculated is equidistant from both of the magnets. This distance can be expressed as $d$.
The magnetic field due to a bar magnet is given by the equation,
$B=\left( \dfrac{{{\mu }_{0}}}{4\pi } \right)\dfrac{M}{{{d}^{3}}}$
As we look into the picture we can see that the point P is located at the exact midpoint between the two magnets. They are placed as opposite to the magnetic field also. Hence the magnetic field by both the bar magnet will be the same. Therefore the total magnetic field at P can be calculated by taking the sum of these magnetic fields.
${{B}_{P}}=\left( \dfrac{{{\mu }_{0}}}{4\pi } \right)\dfrac{M}{{{d}^{3}}}+\left( \dfrac{{{\mu }_{0}}}{4\pi } \right)\dfrac{M}{{{d}^{3}}}=2\left( \dfrac{{{\mu }_{0}}}{4\pi } \right)\dfrac{M}{{{d}^{3}}}$

So, the correct answer is “Option A”.

Note:
The magnetic moment defines the strength of a magnet and the orientation of a magnet or any other object that creates a magnetic field. It is a tendency of getting arranged according to the magnetic field acting. It is a vector quantity. The objects having magnetic moment includes loops of current, permanent magnets etc.