Question

Two identical bar magnets, each having a magnetic moment of $10A{m^2}$ , are arranged such that their axial lines are perpendicular to each other and their centers are along the same straight line in a horizontal plane. If the distance between their centers is $0.2m$ the resultant magnetic induction at a point midway between them is $\left( {\mu_0 = 4\pi \times {{10}^{ - 7}}H{m^{ - 1}}} \right)$
$\left( A \right)\sqrt 2 \times {10^{ - 7}}\,Tesla$
$\left( B \right)\sqrt 5 \times {10^{ - 7}}\,Tesla$
$\left( C \right)\sqrt 2 \times {10^{ - 3}}\,Tesla$
$\left( D \right)\sqrt 5 \times {10^{ - 3}}\,Tesla$

Answer 1

First of all draw a rough diagram as per the given problem statement. Two identical bar magnets are placed perpendicular and according to their arrangement we can write the resultant magnetic induction. Now putting the corresponding values for each bar magnet we will find the solution.

Complete answer:
As per the problem we have two identical bar magnets, each having a magnetic moment of $10A{m^2}$ , are arranged such that their axial lines are perpendicular to each other and their centers are along the same straight line in a horizontal plane. The distance between their centers is $0.2m$ .
We need to calculate the resultant magnetic induction at a point midway between them.
Distance between OO’ is $0.2m$ .

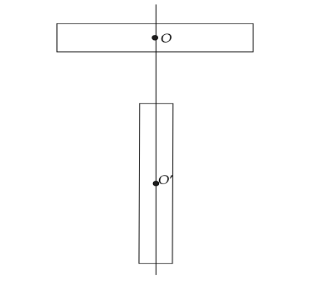
Now using the resultant magnetic induction formula at a point midway we will get,
$B = \sqrt {B{_1^2} + B{_2^2}}$
Where
The magnetic field due to O magnetic is $B_1$ .
And the magnetic field due to O’ magnetic is $B_2$ .
We know magnetic field formula of a bar magnetic is,
$B_2 = \dfrac{{\mu_0}}{{4\pi }} \times \dfrac{{2M}}{{{d^3}}}$ (On axial point)
$B_1 = \dfrac{{\mu_0}}{{4\pi }} \times \dfrac{M}{{{d^3}}}$ (On normal bisector)
Where,
M is the magnetic moment of the bar magnet.
Distance from the center is d.
Now putting the magnetic field of the bar magnet in the resultant magnetic field we will get,
$B = \sqrt {{{\left( {\dfrac{{\mu_0}}{{4\pi }} \times \dfrac{M}{{{d^3}}}} \right)}^2} + {{\left( {\dfrac{{\mu_0}}{{4\pi }} \times \dfrac{{2M}}{{{d^3}}}} \right)}^2}}$
Taking out $\dfrac{{\mu_0}}{{4\pi }}$ as common term we will get,
$B = \dfrac{{\mu_0}}{{4\pi }}\sqrt {{{\left( {\dfrac{M}{{{d^3}}}} \right)}^2} + {{\left( {\dfrac{{2M}}{{{d^3}}}} \right)}^2}}$
Now taking distance d and magnetic moment M as common we will get,
$B = \dfrac{{\mu_0}}{{4\pi }}\sqrt {{{\left( {\dfrac{M}{{{d^3}}}} \right)}^2}\left( {1 + 4} \right)}$
$\Rightarrow B = \dfrac{{\mu_0}}{{4\pi }} \times \dfrac{M}{{{d^3}}}\sqrt {\left( 5 \right)}$
Now putting the know value we will get,
$B = \dfrac{{\mu_0}}{{4\pi }} \times \dfrac{M}{{{d^3}}}\sqrt {\left( 5 \right)}$
Where,
$\dfrac{{\mu_0}}{{4\pi }}$ is equal to ${10^{ - 7}}$ which is a constant term.
$M = 10A{m^2}$
$d = 0.2m$
Now putting above we will get,
$B = {10^{ - 7}} \times \dfrac{{10A{m^2}}}{{{{\left( {0.1} \right)}^3}}}\sqrt {\left( 5 \right)}$
$\Rightarrow B = {10^{ - 7}} \times 10A{m^2} \times {10^3}\sqrt {\left( 5 \right)}$
On solving further we will get,
$B = \sqrt 5 \times {10^{ - 3}}\,Tesla$
Therefore the correct option is $\left( D \right)$ .

Note:
Here we take the distance as $0.1$ meter because we have to calculate the magnetic field in the mid-way of OO’. Remember that the field direction is taken to be outward from the North Pole and inward from the South Pole. And note that these magnetic field lines form a closed path in a bar magnet.