Question

Two identical balls are kept touching each other. Both have a radius R. Find out the relation between their force of gravity and radius:-

(A) $\dfrac{1}{{{R^2}}}$
(B) $\dfrac{1}{{{R^4}}}$
(C) ${R^4}$
(D) ${R^3}$

Answer 1

Hint To solve this question, we have to use Newton's law of Gravitation which relates the force and the distance between two masses. For using this law, we need to convert the two spheres into point masses.

Formula Used: The formula used in this question is given by
$\Rightarrow F = G\dfrac{{{m_1}{m_2}}}{{{r^2}}}$
Here, $F$ is Force of gravitation, $G$ is Universal Gravitational Constant, ${m_1}$ and ${m_2}$ are the two masses, and $r$ is the distance between the two masses.

Complete step by step answer
We use the Newton’s law of gravitation, which is stated as
$\Rightarrow F = G\dfrac{{{m_1}{m_2}}}{{{r^2}}}$ …………………...(i)
Now, as this law is valid for two point masses, so we need to consider the force between the centers of mass of the two spheres.
We know that the centre of mass of a sphere lies at its centre, which carries the whole mass. So the whole mass of the spheres can be assumed to be concentrated at their centers. So, the problem can be represented by the figure as shown below.

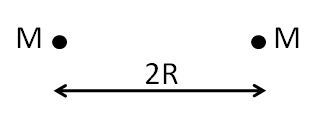
The distance between the two point masses will be equal to the distance between the centers of the original spheres. As the spheres are touching each other, the distance:
$\Rightarrow r = 2R$ ………………..(ii)
Now, as the spheres are identical, their densities are the same. We know that the mass $M$ is related to the density $\rho$ by
$\Rightarrow M = \rho \times V$ ……………………..(iii)
The volume of the sphere is $V = \dfrac{4}{3}\pi {R^3}$
From (iii), the mass of the sphere is
$\Rightarrow M = \rho \times \dfrac{4}{3}\pi {R^3}$
$\Rightarrow M = \dfrac{{4\pi \rho }}{3}{R^3}$
Since both the spheres are of equal radii, so their mass is also equal, i.e.
$\Rightarrow {m_1} = {m_2} = M = \dfrac{{4\pi \rho }}{3}{R^3}$ ……………………...(iv)
Substituting (ii) and (iv) in (i), we get the force between the two spheres as
$\Rightarrow F = G{\dfrac{{\left( {\dfrac{{4\pi \rho }}{3}{R^3}} \right)}}{{{{\left( {2R} \right)}^2}}}^2}$
$\Rightarrow F = \dfrac{{16G{\pi ^2}{\rho ^2}}}{{36}}\dfrac{{{R^6}}}{{{R^2}}}$
On solving, we get
$\Rightarrow F = \dfrac{{4G{\pi ^2}{\rho ^2}}}{9}{R^4}$
From the above expression, we can say that
$\Rightarrow F \propto {R^4}$
Therefore, the force of gravity between the two spheres is proportional to ${R^4}$
Hence, the correct answer is option C.

Note
Do not conclude the answer to this question as $\dfrac{1}{{{R^2}}}$ by directly looking at the expression of Newton’s Gravitational law, since it is inversely proportional to the square of the distance. The inverse square proportion is valid for given values of the mass of the two objects. But in a sphere, the mass is dependent on its radius. So, we obtained the masses in terms of the radii of both the spheres, which is the reason for the different proportionality.