Question
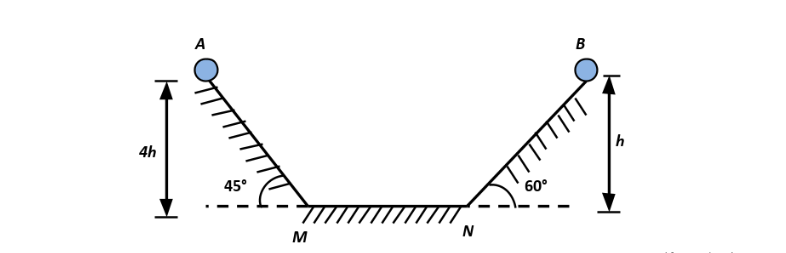
Question: Two identical balls A and B are released from the positions shown in the figure. They collide elas...
Two identical balls A and B are released from the positions shown in the figure. They collide
elastically on horizontal portion MN. The ratio of heights attained by A and B after collision will be
(neglect friction)
A. 1:4
B. 2:1
C. 4:13
D. 2:11
Solution
There are two balls that are identical, they have the same mass. Also, they collide
elastically. Then, by the conservation of momentum, the two balls of identical masses will just exchange their velocities when they collide.
Formula Used: The velocity of a ball at height h is v=2gh
The maximum height attained by the ball in projectile motion is H=2gv2sin2θ
Complete step by step solution: In the diagram, two balls are given that are held at different heights. A ball that is held above the ground has a potential energy that is related to the height above which the object is held. And, if this object is dropped, the Kinetic energy will become the potential energy of motion. These Kinetic energies and potential energies are given by
KE=21mv2and PE=mgh respectively, where mis the mass, vis the velocity
and h is the height of the ball. Thus, velocity of the ball can be calculated as follows
21mv2=mgh→v2=m2mgh=2gh→v=2gh →(1)
Ball A has height 4h and B has h. Let the velocity of ball A be v1 and that of ball B be
v2. Thus, from equation (1)
v1=2g(4h)=8gh and v2=2gh
It is given that the balls are identical and collide elastically, then their velocities will exchange. Now,
after collision, the balls will bounce backwards in the same direction from which they came with
exchanged velocities such that the velocity of ball A will be v2 and that of ball B will be v1.
When they bounce back, ball A will reach only upto height h on the 4h heighted slant plane
because its velocity is v2 and it has potential only to reach the distance h. On the other hand, Ball B has potential to reach the distance 4h. But, the slant plane has height h. Therefore, it will perform a projectile motion and will fall off the plane to the ground.
The angle of the second slant plane is given to be 60∘. Therefore, the ball B will be thrown off the plane making an angle 60∘. The total kinetic energy that ball B contains is
21mv12. This energy can be resolved as
21mv12=mgh+21mv2 →(2)
where, mghis the potential energy of the ball upto height h. Then, the ball will form a projectile.
Let the velocity of the ball while performing the projectile be v. Then the Kinetic energy will be
21mv2 as in equation (2).
Cancelling the mass of the ball from both the sides and substituting the value of v1, then equation(2) will be
21(8gh)=gh+21v2→v2=6gh→v=6gh
The velocity v=6gh is the velocity for the projectile. The maximum height attained by ball B will be
H=2gv2sin2θ
Here, θ=60∘. Therefore, H=2g(6gh)sin2(60∘)=3h×43=49h
Since, sin60∘=23→sin260∘=43
The total height attained by ball B will be hB=h+H=h+49h=413h
The ratio of heights attained by A and B after collision will be
