Question

Two ideal batteries of emf ${V_1}$ and ${V_2}$ and three resistances ${R_1}$ , ${R_2}$ and ${R_3}$ are connected as shown in the figure. The current in the resistance ${R_2}$ will be zero if

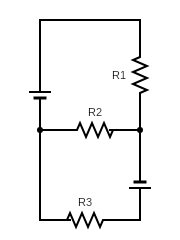
(A) ${V_1} = {V_2}$ and ${R_1} = {R_2} = {R_3}$
(B) ${V_1} = {V_2}$ and ${R_1} = 2{R_2} = {R_3}$
(C) ${V_1} = 2{V_2}$ and $2{R_1} = 2{R_2} = {R_3}$
(D) $2{V_1} = {V_2}$ and $2{R_1} = {R_2} = {R_3}$

Answer 1

Hint
As a convention, for voltage sources, when moving from negative to positive add voltage when moving from positive to negative subtract voltage. For resistors, when moving in the same direction as conventional current, subtract voltage across the resistor but when moving in the opposite direction add voltage across the resistor.
Formula used: $\sum V = 0$ where $V$ is voltage around a loop,
$\sum {{I_{in}} = \sum {{I_{out}}} }$ where ${I_{in}}$ is current going into a node and ${I_{out}}$ is current leaving the node .

Complete step by step answer

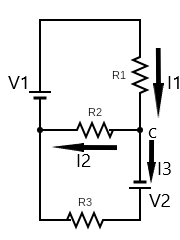
Applying Kirchhoff’s rule to the top loop, we have
${V_1} - {I_1}{R_1} = 0$ where ${I_1}$ is the current flowing through ${R_1}$ and ${I_2}$ is the current flowing through ${R_2}$ .
Similarly, for the bottom loop
$\Rightarrow {V_2} - {I_3}{R_3} + {I_2}{R_2} = 0$
Applying Kirchhoff’s rule at node c, we get
$\Rightarrow {I_1} = {I_2} + {I_3}$
Now if current is not flowing through ${R_2}$ i.e. ${I_2} = 0$ , then the Kirchhoff’s equations become
$\Rightarrow {V_1} - {I_1}{R_1} = 0 \Rightarrow {V_1} = {I_1}{R_1}$
$\Rightarrow {V_2} - {I_3}{R_3} = 0 \Rightarrow {V_2} = {I_3}{R_3}$
${I_1} = {I_3}$
Dividing ${V_1}$ by ${V_2}$ and cancelling out ${I_1}$ and ${I_3}$ since ${I_1} = {I_3}$ we get,
$\Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{{R_1}}}{{{R_3}}}$
Now, we substitute from the options.
For option A, if ${R_1} = {R_3}$ as given, they cancel and we get
$\Rightarrow {V_1} = {V_2}$ which matches the expression as given.
Thus, option A is a solution.
For option B, since ${R_1} = {R_3}$ , irrespective of ${R_2}$ , we still have
$\Rightarrow {V_1} = {V_2}$ which also matches the expression given.
For option C, since $2{R_1} = {R_3}$ , we get
$\Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{{R_1}}}{{2{R_1}}} = \dfrac{1}{2}$
Cross multiplying we get,
$\Rightarrow 2{V_1} = {V_2}$ which does not match the expression given. Thus, C is not a solution.
For option D, since it is given that $2{R_1} = {R_3}$ , then $\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{{R_1}}}{{2{R_1}}} = \dfrac{1}{2}$
Cross multiplying we get
$\Rightarrow 2{V_1} = {V_2}$ which corresponds to the expression given.
Hence, the correct options are option (A) and (D).

Additional Information
Kirchhoff’s rule is a physical principle which is more fundamental than Ohm’s law as it was derived from the principle of conservation of charge. In fact, it works with other elements besides resistors such as capacitors and inductors. It can also be used to analyze low frequency ac current.

Note
The voltage drop in ${R_2}$ was added because the direction of conventional current has already been assumed in the top loop and the bottom loop moves in the direction opposite to this assumed direction.