Solveeit Logo
Login

Question

Question: Two heavy spheres each of mass 100Kg and radius \(0.1m\) are placed 1m apart on the horizontal table...

Two heavy spheres each of mass 100Kg and radius 0.1m0.1m are placed 1m apart on the horizontal table. What is the gravitational field and potential at the midpoint of the line joining the center of the spheres?

Explanation

Solution

Hint : Gravitational field is basically due to the gravitational force exerted by the masses at a given point and is calculated by:
E→=GMr2r^\overrightarrow{E}=\dfrac{GM}{{{r}^{2}}}\widehat{r};
Where G is the gravitational constant, M is the mass of the object and r is the distance of the object from the point where the field is to be calculated. r^\widehat{r} is the direction of the field acting on the point.
Also gravitational potential is given by:
V=−GMRV=-\dfrac{GM}{R}
Here also G, M and R have the same meanings as above. Here potential is a scalar quantity so its direction is not considered.

Complete step by step answer

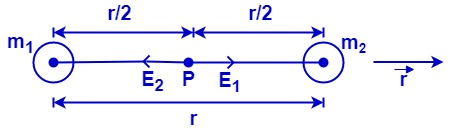
Let P be the point where gravitational field and potential are to be calculated and m1 and m2 be the two masses.
Also let r→\overrightarrow{r}be the default direction of the field.
As P is located at the midpoint of the line joining the centers of the two so its distance from each mass is r/2 where r is the total distance between the two given masses.
Gravitational field acting on P due to mass m1;
E1→=Gm1(r2)2r^\overrightarrow{{{E}_{1}}}=\dfrac{G{{m}_{1}}}{{{\left( \dfrac{r}{2} \right)}^{2}}}\widehat{r}
Similarly, field due to m2;
E2→=Gm2(r2)2(−r^)\overrightarrow{{{E}_{2}}}=\dfrac{G{{m}_{2}}}{{{\left( \dfrac{r}{2} \right)}^{2}}}(-\widehat{r})
Here the negative sign on r^\widehat{r} is due to its opposite direction to the field produced by mass m1.
Enet→=E1→+E2→ Enet→=Gm1(r!!╱!!2  )2r^+Gm2(r!!╱!!2  )2(−r^) Enet→=Gm1(r!!╱!!2  )2r^−Gm2(r!!╱!!2  )2r^ As m1=m2=M=100Kg So, Enet=GM(r!!╱!!2  )2−GM(r!!╱!!2  )2 Enet=0 ........................ (1) \begin{aligned} & \overrightarrow{{{E}_{net}}}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}} \\\ & \overrightarrow{{{E}_{net}}}=\dfrac{G{{m}_{1}}}{{{\left( {}^{r}\\!\\!\diagup\\!\\!{}_{2}\; \right)}^{2}}}\widehat{r}+\dfrac{G{{m}_{2}}}{{{\left( {}^{r}\\!\\!\diagup\\!\\!{}_{2}\; \right)}^{2}}}(-\widehat{r}) \\\ & \overrightarrow{{{E}_{net}}}=\dfrac{G{{m}_{1}}}{{{\left( {}^{r}\\!\\!\diagup\\!\\!{}_{2}\; \right)}^{2}}}\widehat{r}-\dfrac{G{{m}_{2}}}{{{\left( {}^{r}\\!\\!\diagup\\!\\!{}_{2}\; \right)}^{2}}}\widehat{r} \\\ & \text{As }{{\text{m}}_{1}}={{m}_{2}}=M=100Kg \\\ & So, \\\ & {{E}_{net}}=\dfrac{GM}{{{\left( {}^{r}\\!\\!\diagup\\!\\!{}_{2}\; \right)}^{2}}}-\dfrac{GM}{{{\left( {}^{r}\\!\\!\diagup\\!\\!{}_{2}\; \right)}^{2}}} \\\ & {{E}_{net}}=0\text{ }........................\text{ }(1) \\\ \end{aligned}
Now gravitational potential at P due to m1;
V1=−Gm1(r!!╱!!2  ){{V}_{1}}=-\dfrac{G{{m}_{1}}}{\left( {}^{r}\\!\\!\diagup\\!\\!{}_{2}\; \right)}
Similarly
V2=−Gm2(r!!╱!!2  ) Vnet=V1+V2 =−Gm1(r!!╱!!2  )+[−Gm2(r!!╱!!2  )] \begin{aligned} & {{V}_{2}}=-\dfrac{G{{m}_{2}}}{\left( {}^{r}\\!\\!\diagup\\!\\!{}_{2}\; \right)} \\\ & {{V}_{net}}={{V}_{1}}+{{V}_{2}} \\\ & =-\dfrac{G{{m}_{1}}}{\left( {}^{r}\\!\\!\diagup\\!\\!{}_{2}\; \right)}+\left[ -\dfrac{G{{m}_{2}}}{\left( {}^{r}\\!\\!\diagup\\!\\!{}_{2}\; \right)} \right] \\\ \end{aligned}
=−2GMr−2GMr=-\dfrac{2GM}{r}-\dfrac{2GM}{r}
=−4GMr=-\dfrac{4GM}{r}
As G = 6.67×10−11Nm2Kg−2\text{G = }6.67\times {{10}^{-11}}N{{m}^{2}}K{{g}^{-2}}
So,V=−4×6.67×10−11×1001V=-\dfrac{4\times 6.67\times {{10}^{-11}}\times 100}{1}
V=−2.67×10−8JKg−1V=-2.67\times {{10}^{-8}}JK{{g}^{-1}}…….. ….. (2)

Note Keep in view that as the gravitational field is a vector quantity so its direction should also be specified which changes the whole calculation of its magnitude also. Gravitational force depends on both the source mass and test mass while the field is purely a property of the source mass. This vector field clearly depends only on the earth. It measures how much force the earth will exert on a unit mass, hence g sometimes called gravitational force per unit mass.