Question

Two godowns $A$ and $B$ have grain capacity of $100$ quintals and $50$ quintals respectively. They supply to $3$ ration shops, $D,E$ and $F$ whose requirements are $60,50$ and $40$ quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:
Transportation cost per unit quintal (in Rs.)

From/To	$A$	$B$
$D$	$6$	$4$
$E$	$3$	$2$
$F$	$2.50$	$3$

How should the supplies be transported in order that the transportation cost is minimum? What is the minimum cost?

Answer 1

First, we distribute the quantity of quintals sent to each ration shop by each godown by taking two variables as a starter. By applying the given conditions, we get variables for each ration shop. Then we draw a LPP to represent these in order for a good understanding. Then the transportation equation is formed, and the inequalities are formed to represent them in the graph. The coordinates are taken to find the given variables and the transportation is found. The minimum transportation cost coordinates are substituted in the godown supply.

Complete step-by-step solution:
Given two godowns, $A$ and $B$.
Let us assume that the godown $A$ supplies $x$ quintals grain to the ration shop $D$ and $y$ quintals grain to the ration shop $E$.
The remaining quintals of godown A$$$$ = 100 - x - y
These remaining quintals of grain are supplied to the ration shop $F$
Now moving onto the supply from godown $B$
Ration shop $D$ needs only $60$ quintals of grains. Since $x$ quintals of grain is already submitted by the ration shop $A$, the remaining needed quintals $= 60 - x$
These $60 - x$ quintals are supplied from godown $B$.
Similarly,
The godown $B$ supplies,
$50 - y$ quintals for ration shop $E$ and
$40 - (100 - x - y)$, that is $x + y - 60$ quintals of grain for ration shop $F$
We can represent the above given information in the LPP as the diagram shown below;

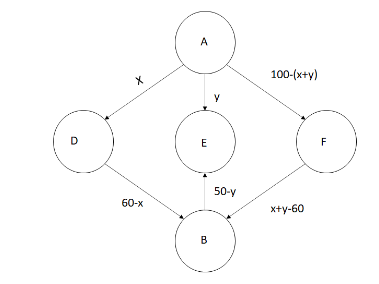
Now, calculating the transportation charges;
Transportation charges of D$$$$ = 6\left( x \right) + 4\left( {60 - x} \right)
$\Rightarrow 6x + 240 - 4x$
$\Rightarrow 2x + 240$
Transport charges of E$$$$ = 3\left( y \right) + 2\left( {50 - y} \right)
$\Rightarrow 3y + 100 - 2y$
$\Rightarrow y + 100$
Transport charges of F$$$$ = 2.50\left( {100 - x - y} \right) + 3\left( {x + y - 60} \right)
$\Rightarrow 250 - 2.x - 2.5y + 3x + 3y - 180$
$\Rightarrow 70 + 0.5x + 0.5y$
Total transportation cost$=$ transportation cost of D$$$$ + transportation cost of E$$$$ + transportation cost of $F$
$\Rightarrow$ Total transportation cost $= 2x + 240 + y + 100 + 70 + 0.5x + 0.5y$
$\Rightarrow$ Total transportation cost $= 2.5x + 2.5y + 410$
Now, godown $A$ can supply only a maximum of $60$ quintals to ration shop $D$ and $50$ quintals to the ration shop $E$, but the maximum quintals being $100$ grain capacity, we have;
$x + y \leqslant 100$
$x \leqslant 60$
$y \leqslant 50$
If godown $A$ supplies $40$ quintals to the ration shop $F$, the remaining quintals are distributed between $D$ and $E$. Then we have;
$x + y \geqslant 60$
And because the amount is in grains, we cannot have negative grains numbers. That implies;
$x \geqslant 0$
$y \geqslant 0$
Plotting the points acquired in the above equations in a graph and taking the coordinates, we get the graph as follows:

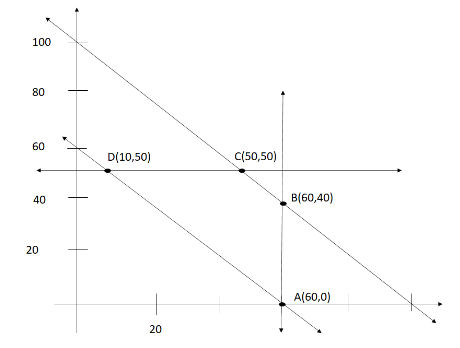
We have the coordinate points-
$A\left( {60,{\text{ }}0} \right)$
$B\left( {60,{\text{ }}40} \right)$
$C\left( {50,{\text{ }}50} \right)$
$D\left( {10,{\text{ }}50} \right)$
Calculating the transportation by substituting the coordinates in the equation $= 2.5x + 2.5y + 410$, we get;

$A{\text{ }}\left( {60,{\text{ }}0} \right)$	$560$
$B{\text{ }}\left( {60,{\text{ }}40} \right)$	$620$
$C{\text{ }}\left( {50,{\text{ }}50} \right)$	$610$
$D{\text{ }}\left( {10,{\text{ }}50} \right)$	$510$

The minimum cost of transportation is $Rs.510$.
That implies;
Godown $A$ to ration shop $D = x = 10$ quintals.
Godown $A$ to ration shop $E = y = 50$ quintals.
Godown $A$ to ration shop $F = 100 - x - y = 40$ quintals.
Godown $B$ to ration shop $D = 60 - x = 50$ quintals.
Godown $B$ to ration shop $E = 50 - y = 0$ quintals.
Godown $B$ to ration shop $F = x + y - 60 = 0$ quintals.

Note: This is done using linear programming. There should be a monitoring of the inequalities of the conditions, taking into consideration every condition that can possibly be applied to the solution. The variables should be respectively taken in correspondence to the acquired coordinates of the graph that is obtained.