Question

Two forces whose magnitudes are in the ratio 3:5 give a resultant of 28N. If the angle of their inclination is ${60^0}$, find the magnitude of each force.

Answer 1

Hint: To solve this question, we will use the method of addition of two vectors. We will use the triangle law of vector addition to find the magnitude of each force when the resultant force is given.
Formula used: $R = \sqrt {{P^2} + {Q^2} + 2PQ\cos \theta }$.

Complete step-by-step solution -
__

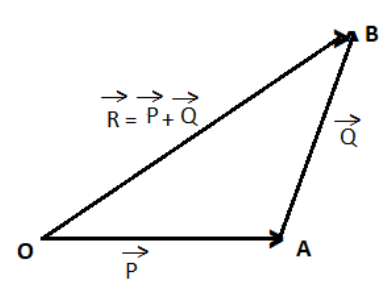
As we know that, by triangle law of vector addition, the magnitude of resultant $\overrightarrow R$ of two vectors $\overrightarrow P$ and $\overrightarrow Q$ inclined to each other at angle $\theta$, is given by
$R = \sqrt {{P^2} + {Q^2} + 2PQ\cos \theta }$.
Here we have given, the ratio of the magnitude of both forces = 3:5
Let the force P = 3x newton and force Q = 5x newton.
Given that, R = 28 newton, and $\theta = {60^0}$.
Now, we know that
$\Rightarrow$ resultant, $R = \sqrt {{P^2} + {Q^2} + 2PQ\cos \theta }$. ……(i)
Putting all values in equation, we get
$\Rightarrow R = \sqrt {{P^2} + {Q^2} + 2PQ\cos \theta } \\\ \Rightarrow 28 = \sqrt {{{(3x)}^2} + {{(5x)}^2} + 2(3x)(5x)\cos {{60}^0}} \\\$
Squaring both sides, we get
$\Rightarrow {(28)^2} = {(3x)^2} + {(5x)^2} + 2(3x)(5x)\cos {60^0} \\\ \Rightarrow 784 = 9{x^2} + 25{x^2} + 30{x^2} \times \dfrac{1}{2} \\\ \Rightarrow 784 = 9{x^2} + 25{x^2} + 15{x^2} \\\ \Rightarrow 784 = 49{x^2} \\\ \Rightarrow \dfrac{{784}}{{49}} = {x^2} \\\ \Rightarrow \sqrt {16} = x \\\ \Rightarrow x = 4 \\\$
Here we get x = 4.
Hence , force P = 3x = 12N and
force Q = 5x = 20N.

Note: Whenever we ask such a question, first we have to remember the concept of addition of vectors. Then we will use that method to find out the required forces when the resultant force and angle inclined are given. After solving we will get the required value of both the forces.