Question

Two forces P and Q have a resultant perpendicular to P. The angle between the forces is:
A. ${\tan ^{( - 1)}}(\dfrac{{ - P}}{Q})$
B. ${\tan ^{( - 1)}}(\dfrac{P}{Q})$
C. ${\sin ^{( - 1)}}(\dfrac{P}{Q})$
D. ${\cos ^{( - 1)}}(\dfrac{{ - P}}{Q})$

Answer 1

Vector quantities are the quantities which have a magnitude as well as direction. We will use the formula of resultant vector to find the angle between the two forces and as the resultant vector is perpendicular to the P vector, the tangent of the angle will diverge and would be equal to infinity and through this relation, we will find the angle between the forces.

Complete step by step answer:

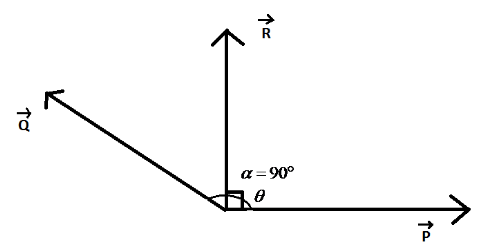
There are two types of quantities: Scalar and vector. Scalar quantities only have magnitude and do not have a specific direction to them. Examples of scalar quantities are distance, speed and temperature.Vector quantities are the type of quantities which have a magnitude as well as direction. Examples of vector quantities are velocity, displacement, force and many more.
Here, $\vec P$ and $\vec Q$are two vectors, particularly force vectors. The angle between the vectors $\vec P$ and $\vec Q$is$\theta$. Now, the resultant vector between these two vectors is perpendicular with respect to$\vec P$. Here, the angle between $\vec P$ and $\vec R$ is taken as $\alpha$. Now, we know that the formula for the angle of the resultant vector of two vectors with respect to one vector is given as:
$\tan \alpha = \dfrac{{Q\sin \theta }}{{P + Q\cos \theta }}$
Where, P and Q are the two vectors, $\theta$ is the angle between the vectors and $\alpha$ is the angle between P vector and the resultant vector. Here, in our case;
$\tan \alpha = \dfrac{{Q\sin \theta }}{{P + Q\cos \theta }}$
But, $\alpha = 90^\circ$ and $\tan \alpha = \tan 90^\circ = \infty$

$$P + Q\cos \theta = 0 \\\ \therefore \theta = {\cos ^{( - 1)}}(\dfrac{{ - P}}{Q}) \\\$$

Thus, option D is the correct answer.

Note: This relation only satisfies if the resultant vector is perpendicular to one of the vectors. If instead of perpendicular, had the resultant was parallel to one of the vectors, then the numerator would have been zero, and hence either there would not have been a second vector, or the two vectors would coincide with each other.