Question
Question: Two forces each of magnitude 'f' and making an angle $\phi$ act on a body, then the resultant force ...
Two forces each of magnitude 'f' and making an angle ϕ act on a body, then the resultant force is
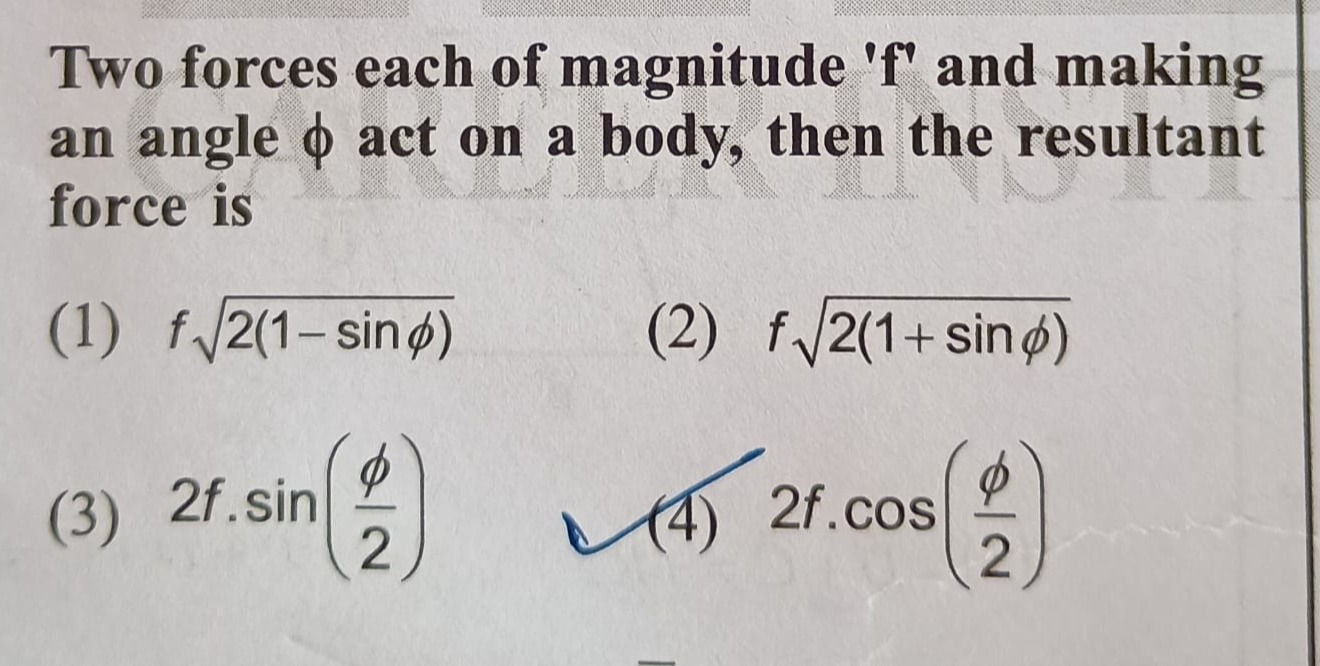
f2(1−sinϕ)
f2(1+sinϕ)
2f.sin(2ϕ)
2f.cos(2ϕ)
2f.cos(2ϕ)
Solution
The magnitude of the resultant force R of two forces of magnitudes F1 and F2 acting at an angle θ is given by the formula:
R=F12+F22+2F1F2cosθ
In this problem, the two forces each have a magnitude f, so F1=f and F2=f. The angle between them is ϕ, so θ=ϕ.
Substituting these values into the formula:
R=f2+f2+2(f)(f)cosϕ R=2f2+2f2cosϕ R=2f2(1+cosϕ)
Now, we use the trigonometric half-angle identity for cosine, which states that 1+cosϕ=2cos2(2ϕ).
Substitute this identity into the expression for R:
R=2f2(2cos2(2ϕ)) R=4f2cos2(2ϕ) R=(2fcos(2ϕ))2 R=∣2fcos(2ϕ)∣
Since the magnitude of the resultant force is always non-negative, and assuming the angle ϕ is between 0 and π (inclusive), 2ϕ will be between 0 and 2π (inclusive). In this range, cos(2ϕ) is non-negative. Thus, ∣cos(2ϕ)∣=cos(2ϕ).
So, the magnitude of the resultant force is:
R=2fcos(2ϕ)
