Question

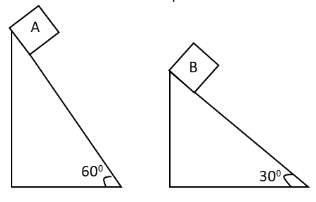
Two fixed frictionless inclined planes making an angle $30^\circ$ and $60^\circ$ with the vertical are shown in the figure. Two blocks A and B are placed on the two planes. What is the relative vertical acceleration of A with respect to B?

A. $4.9\,{\text{m}} \cdot {{\text{s}}^{ - 2}}$ in vertical direction
B. $4.9\,{\text{m}} \cdot {{\text{s}}^{ - 2}}$ in horizontal direction
C. $9.8\,{\text{m}} \cdot {{\text{s}}^{ - 2}}$ in vertical direction
D. Zero

Answer 1

Draw the free body diagram of any block of mass m on an inclined plane with any angle of inclination with the vertical. Apply Newton’s second law of motion to this block in the horizontal direction and determine the value of acceleration. Substitute the value of this acceleration in the formula for vertical acceleration of the block and determine the resultant answer.

Formula used:
The expression for Newton’s second law of motion is
${F_{net}} = ma$
Here, ${F_{net}}$ is net force acting on the object, $m$ is mass of the object and $a$ is acceleration of the object.

Complete step by step answer:
We have given the two fixed frictionless inclined planes making an angle $30^\circ$ and $60^\circ$ with the vertical. We have asked to determine the relative vertical acceleration of A with respect to B. Let us consider any inclined planet having a block on it. Suppose that there is no friction between the block and the inclined plane. Let $m$ be the mass of the block and $a$ be the acceleration of the block. Let us draw the free body diagram of the block on the inclined plane.

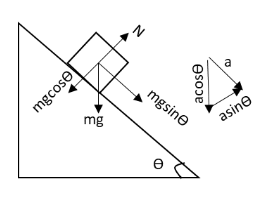
In the above free body diagram, $\theta$ is the inclination of the plane with the vertical, $mg$ is the weight of the block and $N$ is the normal force exerted by the inclined plane on the block. The components of the weight and acceleration are shown in the above free body diagram.

Apply Newton’s second law of motion to the block in the horizontal direction.
$mg\sin \theta = ma$
$\Rightarrow a = g\sin \theta$
Hence, the value of acceleration of the block on the inclined plane is $g\sin \theta$.

From the above free body diagram, we can see that the vertical component of acceleration of the block is
${a_v} = a\sin \theta$
Substitute $g\sin \theta$ for $a$ in the above equation.
${a_v} = \left( {g\sin \theta } \right)\sin \theta$
$\Rightarrow {a_v} = g{\sin ^2}\theta$
Hence, the vertical component of acceleration of the block on any inclined plane is $g{\sin ^2}\theta$.

Let us now determine the vertical acceleration of A with respect to B.
The vertical acceleration of A with respect to B is
$\Rightarrow {a_v} = g{\sin ^2}60^\circ - g{\sin ^2}30^\circ$
$\Rightarrow {a_v} = g\left[ {{{\sin }^2}60^\circ - {{\sin }^2}30^\circ } \right]$
$\Rightarrow {a_v} = g\left[ {{{\left( {\dfrac{{\sqrt 3 }}{2}} \right)}^2} - {{\left( {\dfrac{1}{2}} \right)}^2}} \right]$
$\Rightarrow {a_v} = g\left[ {\dfrac{3}{4} - \dfrac{1}{4}} \right]$
$\Rightarrow {a_v} = \dfrac{g}{2}$

Substitute $9.8\,{\text{m}} \cdot {{\text{s}}^{ - 2}}$ for $g$ in the above equation.
$\Rightarrow {a_v} = \dfrac{{9.8\,{\text{m}} \cdot {{\text{s}}^{ - 2}}}}{2}$
$\therefore {a_v} = 4.9\,{\text{m}} \cdot {{\text{s}}^{ - 2}}$

The acceleration of A with respect to B is $4.9\,{\text{m}} \cdot {{\text{s}}^{ - 2}}$ in the vertical direction.Hence, the correct option is A.

Note: The students may forget to consider the value of vertical acceleration of A as the final required answer. But the students should keep in mind that we have asked to determine the acceleration of the A with respect to B not the vertical acceleration of only A and the ultimate direction of the acceleration is I the vertical direction as we have asked the vertical component of the acceleration of the block.