Question

Two fixed charges $- 2Q$ and $Q$ are located at the points with coordinates $\left( { - 3a,0} \right)$ and $\left( { + 3a,0} \right)$ respectively in the $xy$ plane.
a. Show that all the points in the $xy$ plane where the electric potential due to the two charges is zero lie on a circle. Find its radius and the location of its center.
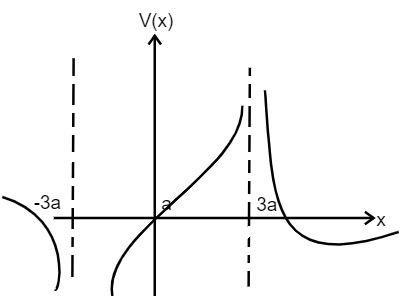
b. Give the expression $V\left( x \right)$ at a general point on the $x$ axis and sketch the function $V\left( x \right)$ on the whole $x$ axis.
c. If a particle of charge $+ q$ starts from rest at the center of the circle, show by a short quantitative argument that the particle eventually crosses the circle. Find its speed when it does so.

Answer 1

Use the formula of the potential of the point charges and equate it to zero to find whether it forms the circle equation. Consider the points in the $x$ axis, in which the potential varies by equation the potential to the zero. Use the conservation of energy formula to find the velocity of the charge.
Useful formula:
(1) The formula of the potential due to point charge is given by
$V = \dfrac{{KQ}}{r}$
Where $V$ is the potential due to the point charge, $K$ is the constant, $Q$ is the point charge and $r$ is the radius of the circle.
(2) The formula of the kinetic energy is given by
$\Rightarrow$ $KE = \dfrac{1}{2}m{v^2}$
Where $KE$ is the kinetic energy of the charge, $m$ is the mass of the charge and $v$ is its velocity.

Complete step by step solution:
(a) Let us consider a point $P$ in the $xy$ plane at which the two point charges $- 2Q$ and $Q$ are located at the $A$ and $B$ respectively. Let us consider that the potential due to these two fixed charges is zero.
$V = 0 \\\ \dfrac{{KQ}}{r} = 0 \\\$
Substituting the charge and the radius in the above step, we get
$\Rightarrow$ $\dfrac{{K\left( { - 2Q} \right)}}{{\sqrt {{{\left( {3a + x} \right)}^2} + {y^2}} }} + \dfrac{{K\left( { - 2Q} \right)}}{{\sqrt {{{\left( {3a - x} \right)}^2} + {y^2}} }} = 0$
Simplifying the above step, we get
$\Rightarrow$ ${\left( {x - 5a} \right)^2} + {y^2} = 4{a^2}$
Hence all the points lie on the circle of the center $\left( {5a,0} \right)$ and radius $4a$ .

(b) Let us consider the point for $x > 3a$
$\Rightarrow$ $V = \dfrac{{KQ}}{{x - 3a}} - \dfrac{{2KQ}}{{x + 3a}} \\\ V = \dfrac{{KQ\left( {9a - x} \right)}}{{{x^2} - 9{a^2}}} \\\$ …………………(1)
For the value of the $- 3a < x < 3a$
$\Rightarrow$ $V = \dfrac{{KQ}}{{3a - x}} - \dfrac{{2KQ}}{{x + 3a}} \\\ V = \dfrac{{KQ3\left( {x - a} \right)}}{{9{a^2} - {x^2}}} \\\$ …………………(2)
For the value of the $x < \- 3a$
$\Rightarrow$ $V = \dfrac{{KQ}}{{3a - x}} - \dfrac{{2KQ}}{{ - 3a - x}} \\\ V = \dfrac{{KQ3\left( {x - a} \right)}}{{9{a^2} - {x^2}}} \\\$ …………….(3)
From the equation (1), (2) and (3), it is clear that the value of $V \ne 0$ and is negative for $x < \- 3a$ .

(c) Let us apply the conservation of the momentum at the center and the circumference.
${\left( {KE + PE} \right)_{{\text{center}}}} = {\left( {KE + PE} \right)_{{\text{circumference}}}}$
The charge starts to move at the circumference only. In the centre it remains fixed.
$\Rightarrow$ $0 + K\left[ {\dfrac{{Qq}}{{2a}} - \dfrac{{2Qq}}{{8a}}} \right] = \dfrac{1}{2}m{v^2} + K\left[ {\dfrac{{Qq}}{{6a}} - \dfrac{{2Qq}}{{12a}}} \right] \\\ \dfrac{1}{2}mv = \dfrac{{KQq}}{{4a}} \\\ v = \sqrt {\dfrac{1}{{4\pi { \in _0}}}\left( {\dfrac{{Qq}}{{2ma}}} \right)} \\\$
Hence the velocity of the charge is obtained as $\sqrt {\dfrac{1}{{4\pi { \in _0}}}\left( {\dfrac{{Qq}}{{2ma}}} \right)}$ .

Note: Remember that the kinetic energy of the charge at the centre of the circle is zero but it has potential energy. This is because at the centre, the charge is fixed but at the circumference it moves with some velocity. $3a + x$ and $3a - x$ are taken, since the charge $- 2Q$ and $Q$ are at $x$ distance from the zero.